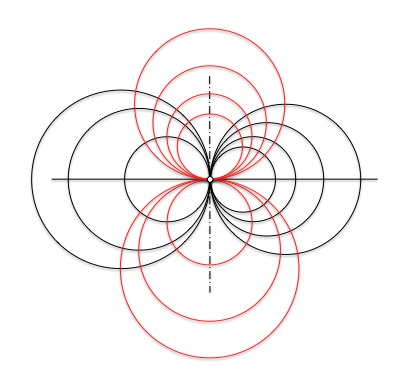
Al definir un haz de circunferencias como un conjunto simplemente infinito que cumplían una restricción basada en la potencia, clasificábamos los haces en función de la posición relativa de sus elementos.
Al definir un haz de circunferencias como un conjunto simplemente infinito que cumplían una restricción basada en la potencia, clasificábamos los haces en función de la posición relativa de sus elementos.
Los haces de circunferencias hiperbólicos se encuentran entre estas familias de circunferencias. De los tres tipos existentes (elípticos, parabólicos e hiperbólicos) son los que ofrecen mayor dificultad en su conceptualización al no venir definidos por puntos de paso. Veremos cómo determinar elementos que les pertenecen tal y como realizamos en los casos anteriores.
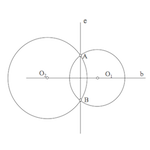
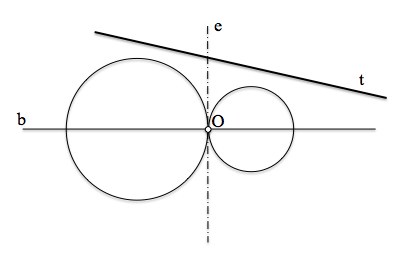
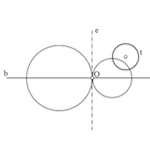
Dadas dos circunferencias no secantes entre sí, el eje radical “e” de las circunferencias es el lugar geométrico de puntos del plano que tienen igual potencia respecto de ambas circunferencias. Esta recta es perpendicular a la que contiene los centros de las circunferencias, y contiene a los centros de las circunferencias ortogonales (perpendiculares) a las del haz.
Dadas dos circunferencias no secantes, podemos determinar una circunferencia ortogonal a ambas con centro el punto O de intersección entre su eje radical e y la recta base b que contiene a ambos centros. El punto O se conoce con el nombre de centro del haz.
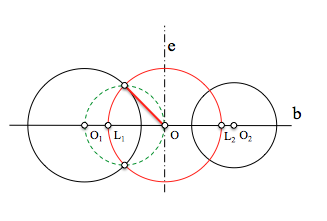
Para ello determinaremos la tangente desde O (centro del haz) a cualquiera de las circunferencias. Esta circunferencia es ortogonal a ambas por tener el radio igual a la raiz de la potencia desde O, y corta en dos puntos L1 y L2 a la recta base, denominados puntos límites, que son a su vez circunferencias del haz.
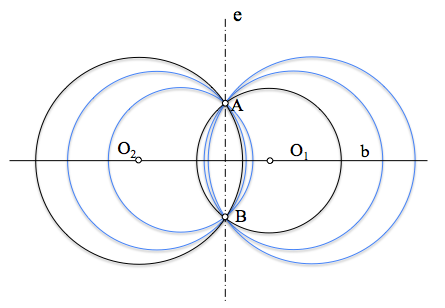
Las infinitas circunferencias de un haz de circunferencias hiperbólico son ortogonales a la que tiene su centro en el del haz, O, y radio la potencia desde este punto a cualquiera de las circunferencias. Los puntos límites son circunferencias del haz de radio nulo.
El eje radical de cualquier pareja de circunferencias de este haz es la recta e.
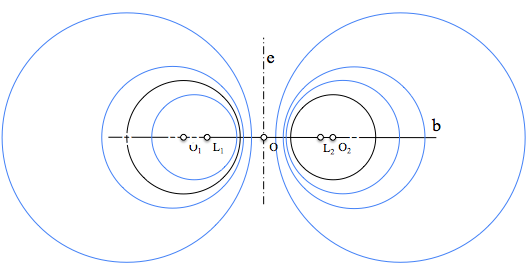
Todos los centros de las circunferencias del haz se encuentran en una recta, b, denominada recta base del haz.
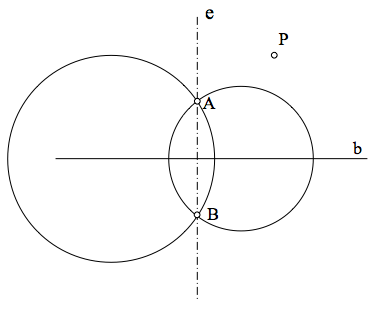
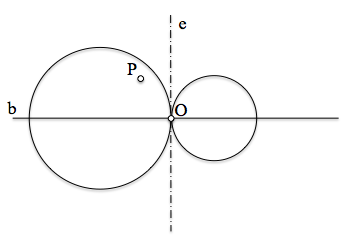
Determinar una circunferencia del haz hiperbólico que pasa por un punto P
De las infinitas circunferencias de una haz elíptico, sólo una pasa por un punto dado. Veamos cómo determinar el centro de una circunferencia del haz que pase por un punto P cualquiera.

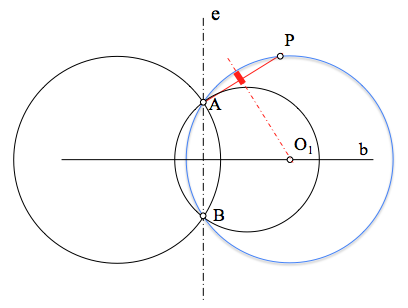
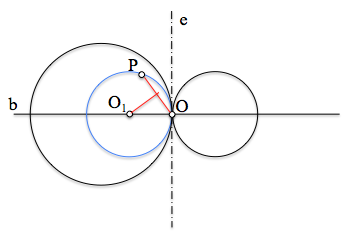
La circunferencia buscada tendrá su centro
O1 en la recta base,
b, y será ortogonal a cualquier circunferencia que pase por los puntos límites.
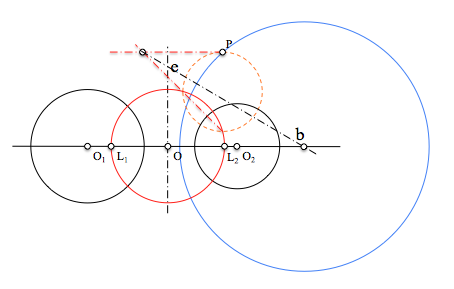
La solución, su centro, se determina por lo tanto mediante la intersección de dos lugares geométricos, la recta base y el eje radical del punto de paso y una circunferencia ortogonal al haz (cualquiera de las que pasa por los puntos límites).
Determinar las circunferencias del haz hiperbólico que son tangentes a una recta dada
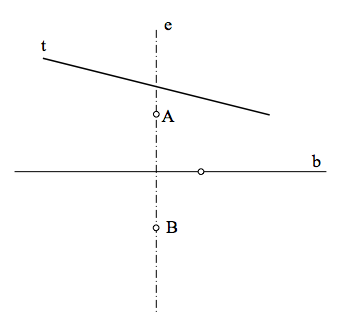
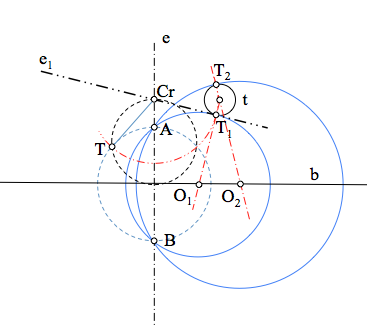
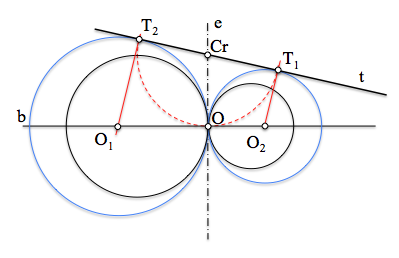
La condición de tangencia viene determinada por una recta t cualquiera que no coincida ni con la recta base b ni con el eje radical e. El haz puede quedar definido por sus puntos límites L1 y L2 o por dos de las circunferencias que le pertenecen.
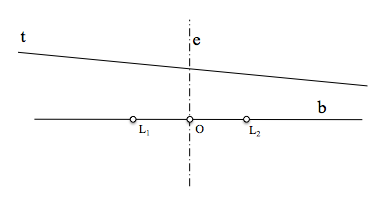
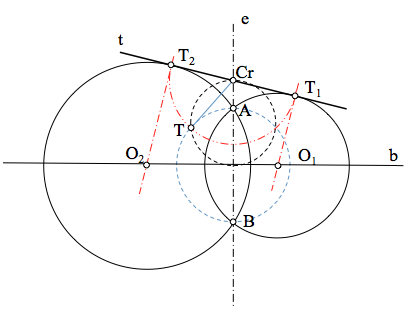
Para resolver el problema buscaremos un punto Cr, del eje radical e, que tenga igual potencia respecto de las circunferencias del haz, y que pertenezca, a su vez, a la recta t ya que ésta última es el eje radical de las circunferencias que le son tangentes. Vemos pues, que Cr es el centro radical de la recta t (circunferencia de radio infinito) y las circunferencias del haz parabólico.
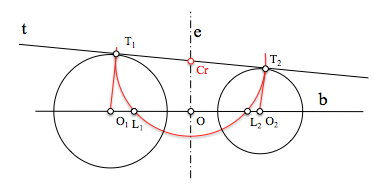
Como se aprecia en la figura, la potencia de Cr respecto de todas las circunferencias del haz la podemos determinar encontrando la tangente (al cuadrado) a cualquier circunferencia del haz (en este caso lla distancia a los puntos límites). Esta distancia es la que habrá también a los puntos de tangencia de las soluciones buscadas. Tenemos dos soluciones ya que podemos llevar esta distancia Cr-L1 a ambos lados de Cr sobre la recta t.
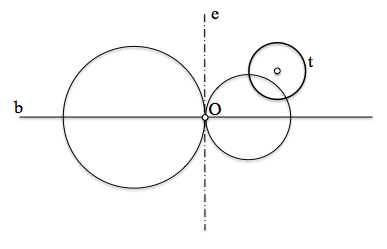
Determinar las circunferencias del haz hiperbólio que son tangentes a una circunferencia dada
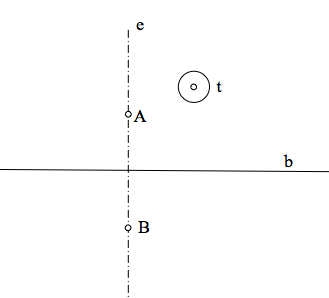
La generalización del problema la tenemos cuando la condición de tangencia es respecto de una circunferencia t cualquiera.
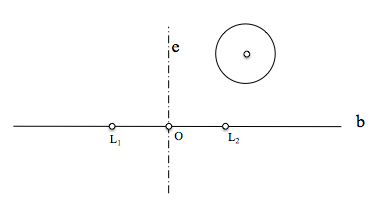
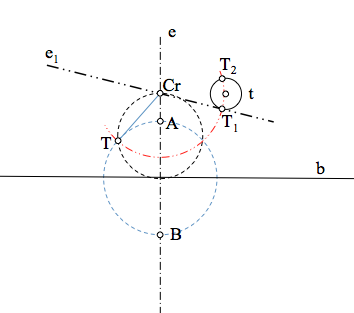
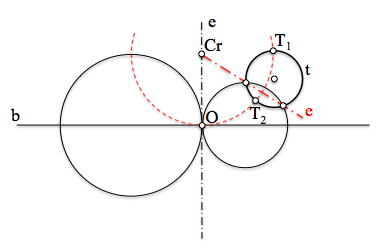
En este caso, de nuevo, determinaremos un punto Cr que tenga igual potencia respecto de la circunferencia que marca la condición de tangencia y cualquiera de las del haz hiperbólico (por ejemplo los puntos límites), por lo que debe encontrarse en su eje radical.
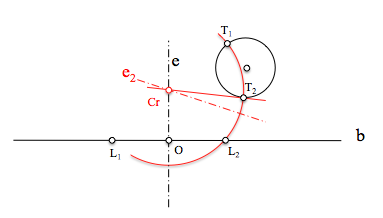
Las soluciones pasarán por los puntos T1 y T2 situados sobre las tangentes trazadas desde Cr, ya que se encuentran a distancia la raíz de la potencia que hemos calculado como en el caso anterior.
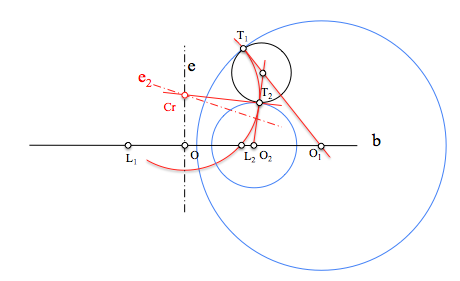
Los centros de las soluciones se encontraran alineados con el centro de la circunferencia t y los correspondientes puntos de contacto.
Haz conjugado
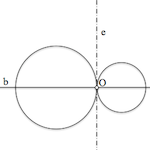
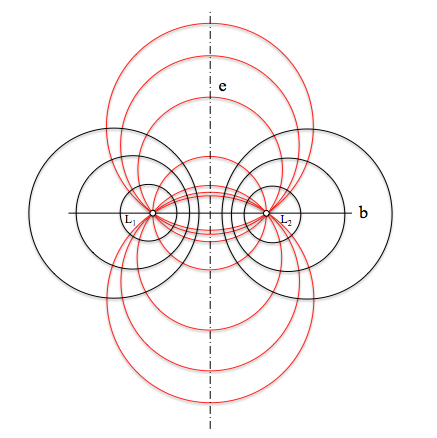
Por último, podemos ver en la figura siguiente el haz conjugado (ortogonal) de un haz hiperbólico, que, como analizaremos posteriormente, es otro elíptico de recta base el eje radical del anterior. Vemos que los puntos límites del haz hiperbólico coinciden con los puntos fundamentales del elíptico.
Geometría métrica
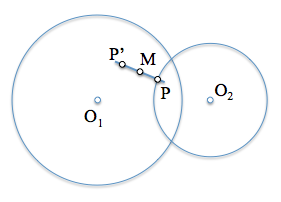
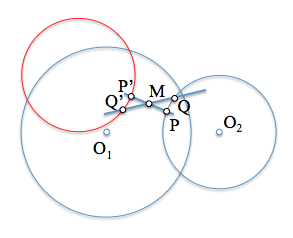
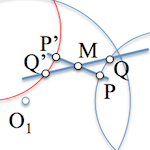 Al plantear un problema de geometría métrica podemos abordar su resolución con diferentes estrategias. para ilustrar uno de estos métodos vamos a resolver el de determinar un segmento del que se conoce su punto medio junto con otras restricciones adicionales.
Al plantear un problema de geometría métrica podemos abordar su resolución con diferentes estrategias. para ilustrar uno de estos métodos vamos a resolver el de determinar un segmento del que se conoce su punto medio junto con otras restricciones adicionales.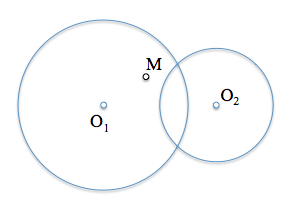





 Circunferencias de un haz hiperbólico tangentes a una recta[/caption]
Circunferencias de un haz hiperbólico tangentes a una recta[/caption]