Geometría y origami [ Libro ]

Geometría y origami es un libro de Stella Ricotti publicada por Homo Sapiens que transmite "felicidad" desde el mundo de las matemáticas. Su autora nos conduce al mundo de la geometría "jugando" desde las bases topológicas que subyacen en una hoja de papel.

Un recurso didáctico sin duda de gran valor que se puede introducir en diferentes niveles educativos; permite "tocar" la matemática desde la concreción de los modelos geométricos que expresan su perfección.

El libro ... "pretende constituirse como un aporte a los docentes de Matemática, tanto de escuelas primarias como medias, y a alumnos de profesorado, para que cuenten con una herramienta más para incursionar placenteramente por el mundo de la Geometría y se animen a pensar nuevas situaciones en el espacio tanto bi como tridimensional".

Tras leer una interesante entrevista con esta profesora, no puedo por menos que estar completamente de acuerdo con su visión de la matemática ligada a la geometría:

-¿Es la geometría "la Cenicienta" de la matemática?

-Más que la Cenicienta, es la Bella Durmiente de las matemáticas. Las tendencias en educación matemática de los años '60 y '70 hicieron que la geometría se sustituyera por un mayor cultivo del álgebra. Como consecuencia, los problemas interesantes de la geometría elemental se ausentaron; la carencia de intuición espacial es una consecuencia observable en las personas que se formaron a partir de esos años. Hoy los docentes estamos haciendo grandes esfuerzos para despertar a la Bella; que nos vuelva a sonreir en las aulas con aires renovados, con miras a formar mentes se desempeñen con ductilidad en este siglo en el que lo visual tiene tanta fuerza. (La Capital.com.ar)

Product Details (Amazon) Publisher: HOMOSAPIENS (2010) Language: Spanish ISBN-10: 9508086424 ISBN-13: 978-9508086426

• Origami : Cómo hacer un libro


• Origami: Principios topológicos [TED]

Geometría métrica: Circunferencias con condiciones angulares. Solución al Problema I

De las diferentes soluciones que se pueden dar al problema propuesto de obtención de circunferencias con condiciones angulares ( que pasan por un punto, son tangentes a una circunferencia y forman un ángulo con una recta), vamos a analizar aquella solución que utilice la aplicación de los conceptos de potencia utilizados en el "Problema Fundamental de Tangencias" ( PFT ).

Posteriormente podremos analizar caminos específicos a este problema concreto que pudieran simplificar su trazado o conceptualización geométrica.

En este último sentido cabe destacar que una construcción geométrica dada, un conjunto de líneas, pueden interpretarse de diferentes formas atendiendo al razonamiento abstracto aplicado al problema.

La búsqueda de modelos generalistas puede ser el primer paso formativo de un geómetra.

Sobre la modificación del enunciado del problema

El primer paso, aplicando el método lógico geométrico o metodología de trabajo expuesta, consistirá en cambiar las condiciones geométricas del problema por otras que sean equivalentes.

De forma general, trataremos de imponer condiciones idénticas cuando se trate de restricciones angulares para convertir las restricciones en "isoangularidad". En este caso, cambiaremos la condición de formar un ángulo de 45º con una recta por la de ser tangente a otra, ya que tenemos una condición de tangencia respecto de la circunferencia. Vemos que el enunciado cambiará a:

Determinar una circunferencia que es tangente a una recta y una circunferencia y pasa (es tangente) por un punto.

De forma análoga se podía haber cambiado la condición de tangencia por una angular a 45º, aunque este concepto ahora parezca más complejo y no sea el camino empleado.

[caption id="attachment_15135" align="aligncenter" width="493"] Grafo inicial con los datos del problema[/caption]

Enunciado modificado equivalente

En efecto, si la circunferencia buscada forma un ángulo con la recta r, su tangente t en el punto de contacto debe formar ese ángulo con r, tal y como vimos al definir el ángulo entre recta y circunferencia.

Nuestro problema consistirá por tanto en determinar una circunferencia tangente a otra y a una recta en uno de sus puntos.

[caption id="attachment_15136" align="aligncenter" width="569"] Enunciado modificado con condiciones de isogonalidad (Apolonio)[/caption]

El problema de isogonalidad que queda es una de las variantes del conocido como "Problema de Apolonio" que proponía la determinación de una circunferencia tangente a tres circunferencias dadas.

¿Tres circunferencias? En efecto, el punto de paso puede ser considerado como una circunferencia de radio cero (nulo) y la recta "t" otra de radio infinito. Este tipo de razonamiento permite agrupar por lo tanto este problema en otro más general de forma sencilla, como planteábamos al principio.

Su solución puede por tanto deducirse del modelo general, con la correspondiente generalización, o pueden incluirse simplificaciones debido a la naturaleza de las restricciones.

Planteamiento de la solución particularizada

Las circunferencias tangentes a la recta t en el punto P tendrán su centro en una recta perpendicular a t por el punto P. Determinan un haz parabólico de circunferencias con eje radical la recta t.

La recta s es el lugar geométrico de los centros de circunferencias que son tangentes a la recta r en el punto P.

Por último determinaremos el centro de la circunferencia solución (azul) que completa el problema. Para ello determinaremos la circunferencia que es tangente a la recta t en el punto P y es tangente a su vez a la circunferencia c1,

Si determinamos una circunferencia cualquiera que sea tangente a la recta t en el punto P y que corte a la circunferencia c1 en un par de puntos (A y B), estaremos obteniendo una de las circunferencias del haz parabólico mencionado.

El punto "I" de intersección de la recta A-B y la recta t es el centro radical de las circunferencias tangentes a t y que pasan por A y B, teniendo por tanto igual potencia respecto de todas ellas. Este valor de potencia es la distancia al punto P de tangencia al cuadrado, y permite por tanto determinar el punto T de tangencia en c1.

Faltaría el análisis del número de soluciones al problema genérico de determinar circunferencias que formen un ángulo con la recta, pasen por un punto y sean tangentes a la circunferencia. De las posibles soluciones que vendrán siempre en parejas, deberemos elegir aquella que se adapte al croquis determinado en el enunciado.

En general, en un problema de tangencias respecto de tres circunferencias, (problema de Apolonio), tendremos hasta 8 soluciones. En este caso se limitan a dos al degenerar una circunferencia en recta y otra en un punto.

¿Puedes resolver este ejercicio con otro modelo diferente? Mejor que hacer muchos ejercicios iguales, planteate resolver el mismo de muchas formas diferentes !!!

Los conceptos de inversión son de especial aplicación en estos problemas, como se ha visto en la "Aplicación a la resolución de problemas de tangencias y angulares"

Geometría métrica

Geometría métrica: Circunferencias con condiciones angulares. Problema I

Los problemas geométricos se pueden abordar con diferentes estrategias para simplificar su análisis y resolución. Normalmente podemos encajarlos en familias estructuradas de problemas además de encontrar soluciones específicas que se adapten a cada problema en particular.

Veamos un problema básico de geometría "vestido" o "adaptado" a una aplicación tecnológica, en particular supongamos que para la definición de una pieza necesitamos unas condiciones geométricas dadas por restricciones angulares.

Enunciado del problema

Completar el diseño de la pieza representada en el croquis sabiendo que la circunferencia c es tangente a c1, pasa por el punto P y corta con un ángulo de 45º a la recta r.

[caption id="attachment_15122" align="aligncenter" width="366"] Croquis para el enunciado gráfico del problema geométrico[/caption]

Datos del problema

Para resolver el problema se nos facilitarán parte de los datos de forma gráfica. Así, en este caso, tendríamos:

[caption id="attachment_15123" align="aligncenter" width="493"] Enunciado problema geométrico[/caption]

Las circunferencias concéntricas con c1 no son relevantes y podemos prescindir de ellas.

Del análisis del enunciado y de los datos gráficos vemos que debemos completar la figura determinando una circunferencia que cumple tres restricciones geométricas:

• Pasa (o pertenece) por el punto P


• Forma un ángulo (45) con la recta r


• Es tangente a la circunferencia c1.

Vemos que la circunferencia que debemos determinar se encuentra restringida por un número de condiciones idéntico al número de datos necesarios para su definición (dos del centro y uno del radio), y que ademas estos datos no son redundantes (combinación lineal) y por tanto son independientes entre sí, por lo que esta circunferencia se encuentra paramétricamente determinada o, lo que es lo mismo, el problema está correctamente propuesto.

Se deja al lector un primer análisis del problema.

Se sugiere tratar de convertir las condiciones angulares en condiciones de isogonalidad (igual ángulo) en particular de tangencias para tratar de reducir el problema al que hemos denominado "Problema Fundamental de Tangencias".

Puedes consultar la solución aquí

Apuesta geométrica [ Alumnos ]

Recuperando algunos artículos de mis alumnos, que pudieran desaparecer al borrar sus blogs de la experiencia de innovación educativa, he visto este del grupo pi-tágoras que une los polígonos y lo lúdico de forma muy acertada.

El enfoque educativo en forma de competición es un valioso recurso que no tiene que hacer perder la rigurosidad en los planteamientos formativos. Al contrario, permite explorar el conocimiento de forma crítica y a la par entretenida. Este grupo de alumnos ha acertado en su enfoque, que ya citamos en su día.

Empezamos un nuevo curso y qué mejor manera de hacerlo que aprender de nuestros alumnos

Apuesta geométrica

El otro día, estando en el lugar más propicio para el intercambio libre de ideas, vamos, en lo que viene siendo el bar, se propuso el siguiente juego, que proponemos a todos los lectores.

• Un señor, bastante mayor, por cierto, nos dió, diez monedas de un euro, y nos dijo: -Si sois capaces de hacer con esas diez monedas, cinco filas de cuatro monedas cada fila, no solo os dare los 10 euros, si no que además os invito a lo que queráis ahora mismo-.

Pobres de nosotros, felices pensando: "bah, estudiantes como nosotros, lo sacamos fijo".El caso, pasó una hora y no sacamos nada en claro.

• Seguros de nuestras capacidades y con cara de indignación, miramos a aquel señor y le dijimos: -Esto es imposible- a lo que el contestó: -Cierto se me olvidaba deciros que una moneda puede pertenecer a varias filas, eso si, no me hagaís una fila de diez monedas y me la subdividais-.

Ahora si es nuestro pensamos. Pobres de nosotros, otra vez. El partido concluyó (que si, que fuimos a ver el partido) y el señor anunció que se marchaba, llevandose las monedas y la solución. Horas más tarde, y ya en casa, se paseó, por la mente de algunos la solución. Una solución geométrica (¡que casualidad!).

Querido lector, si quiere pensar la solución, le recomendamos que no pase de estas líneas por que sera aquí donde se exponga (y donde por fin empecemos a hablar de dibujo, que ya esta bueno...).

-----------------------------------------------------------------------------------------

Como tantas veces hemos hecho en la clase de dibujo, debemos simplificar el problema que se nos pide resolver, en uno mucho más sencillo.

En este caso ocurre lo mismo, y para el análisis y resolución de este problema seguiremos un procedimiento análogo.

Trataremos las monedas como puntos, y las filas no seran otra cosa que segmentos determinados por esos puntos. Así se nos pide determinar cinco segmentos conocidos diez puntos, y que cada segmento este formado por cuatro puntos, es decir, cada punto será común a dos segmentos.

Obviamente, y como ya hemos indicado, esto no es general para cualesquiera diez puntos, si no que el problema reside en encontrar la posición específica en la que esto se cumple. Comencemos ahora el análisis de este interesante problema.

Si seleccionamos 10 puntos en el plano, no alineados estoy seguro de que a la mayoría de las personas les viene a la mente la idea de un polígono, un polígono de diez lados.

Cuando nos piden hacer cinco líneas, con puntos pertenecientes a varias lineas a muchos se nos ocurre la idea de varios trazados con un punto común como dos rectas que se cortan en un punto.

[caption id="attachment_15033" align="alignleft" width="150"] Pentagono[/caption]

Y a partir de estas ideas comenzamos a pelearnos con este pequeño juego geométrico.

Llevando a la situación límite esta idea de las rectas,llega un momento en el cual, como tenemos que situar cinco segmentos se nos ocurre situar cinco puntos, sabiendo que con esos cinco puntos, comunes todos a dos segmentos quedan totalmente determinados los cinco segmentos, observamos que cinco puntos definen un polígono de cinco lados:

un pentágono.

Pero aún nos quedan otros cinco puntos que determinar, y todos ellos comunes a dos segmentos, es ahora cuando entra en juego la idea de el polígono estrellado inscrito al pentágono.

Nos centramos ahora en nuestro polígono estrellado inscrito al pentágono.

Ya tenemos colocadas nuestras rectas en cuyas intersecciones estarán los puntos, y con ellos determinados los segmentos.

Volviendo al problema inicial habremos determinado, cinco filas de cuatro monedas cada fila.

Sinceramente, nosotros nos quedamos sin dinero y sin consumición, asi que, por lo menos esperamos que os haya gustado.

Un saludo, pitagorines.

La geometría de chicle [ Alumnos ]

Uno de los primeros artículos que escribieron mis alumnos del grupo "Catetos de la Geometría" fue sobre los aspectos más básicos de la geometría: la topología. A ellos les resultó curioso el concepto y, sin darse cuenta, estaban profundizando en los principales aspectos que configuran un sistema lógico axiomáticos geométrico: la continuidad.

Empezábamos la experiencia de innovación educativa introduciendo los blogs como herramienta dinamizadora del grupo y nos encontrábamos con esta perla. No dejaré de aprender de ellos.

Os dejo su artículo, tal y como lo escribieron. (Por cierto, el vídeo es genial)

LA GEOMETRÍA DE CHICLE

- ¿Cuántos lados tiene una circunferencia?
- Dos, el de dentro y el de fuera.

Aunque parezca un chiste matemático, a lo largo de esta entrada descubriréis que no lo es del todo.Hablamos de topología: es una rama de la geometría que estudia únicamente las propiedades de los cuerpos geométricos que permanecen invariantes cuando sufren transformaciones.

Es una geometría sin medidas, llamada también geometría de la membrana de goma o del chicle, puesto que las figuras siguen siendo las mismas aunque las sometamos a deformaciones (retorcer, distorsionar, estirar, contraer...) pero sin desgarramientos ni roturas: es como si estuvieran hechas de goma o plastilina.

Por ejemplo, el tamaño y la forma no son propiedades topológicas: un globo se puede hinchar o deshinchar, deformarse en un cubo o tomar la forma de una jirafa sin necesidad de desgarrarlo.
Sin embargo, una cuerda que está unida por las dos partes con un nudo o no, sería una propiedad topológica. Una de estas propiedades de las curvas en el espacio, es que una curva cerrada divide al plano que la contiene en dos partes: la interior y la exterior.

El número de dimensiones de una figura, la proximidad, el tipo de textura, el hecho de tener o no borde, el número de agujeros... son también propiedades topológicas.

El número de agujeros que presenta una figura es lo que se conoce como su género (es el número máximo de cortes que se le puede hacer sin partirla en dos trozos).

• Una esfera maciza es de género 0, puesto que carece de agujeros y sólo es necesario un corte para romperla en dos partes.


• Una rosquilla tiene género 1, pues tiene un agujero y se le puede hacer un corte sin romperlo en dos pedazos.


• Unas gafas sin cristales tienen género 2, porque al tener dos agujeros se les pueden hacer dos cortes sin romperlas en dos partes.

Una esfera, un cubo y una pirámide son topológicamente lo mismo porque podríamos transformar uno en otro sin necesidad de romper ni unir sus partes.
Sin embargo, una circunferencia no es lo mismo que un segmento, puesto que habría que partirla por algún punto.Un ejemplo típico es el de la rosquilla y la taza de café, figuras topológicamente equivalentes, de género 1.

Y si lo pensáis, los seres humanos también somos de género 1.

Somos topológicamente equivalentes a las rosquillas: nuestro tubo digestivo correspondería al agujero de un donut.

Aquí os dejo un curioso vídeo:

La topología es por supuesto una disciplina matemática, y como tal, a menudo en el trabajo teórico no hace falta tener un método para encontrar la solución, sino que lo importante es saber que existe tal solución.
Por ejemplo, siempre hay un par de puntos diametralmente opuestos (antipodales) sobre la superficie de la Tierra que tienen exactamente la misma temperatura y presión. Estos puntos van variando y no hay manera de encontrarlos, pero podemos demostrar que existen siempre.

Históricamente, las primeras menciones a una geometría sin medidas proceden de Leibniz, quién la llamógeometría de la posición. Pero no es hasta la resolución del famoso problema de los puentes de Königsberg por parte de Euler, cuando se habla de "topología".

Aquí tenéis más temas relacionados en los blogs de nuestros compañeros: problema de los puentes de Königsberg y Cinta de Möbius .

Zaha Hadid y el Deconstructivismo

Zaha Hadid es una arquitecta, diseñadora y urbanista contemporánea que diseña formas innovadoras que rebosan fantasía evocando mundos futuros.

En las páginas web de Zaha Hadid podemos ver una impresionante muestra de su ideación, que se mueve en los límites del deconstructivismo. Curvas sinuosas que transmiten un sentimiento orgánico diferente en estas disciplinas.

Zaha Hadid (árabe: زها حديد) (Bagdad; 31 de octubre de 1950 - ) es una prominente arquitecta angloiraquí, procedente de la corriente del deconstructivismo. A pesar de ser de nacionalidad iraquí, la mayor parte de su vida la ha pasado en Londres, donde se ubica su estudio de arquitectura. La obra arquitectónica de Zaha Hadid ha sido reconocida en diversas ocasiones con premios de rango internacional entre ellos el Premio Pritzker, tratándose de la primera mujer que consigue este galardón.(W)

[caption id="attachment_14972" align="aligncenter" width="176"] Belu Bench[/caption]

El deconstructivismo, también llamado deconstrucción, es un movimiento arquitectónico que nació a finales de la década de 1980. Se caracteriza por la fragmentación, el proceso de diseño no lineal, el interés por la manipulación de las ideas de la superficie de las estructuras y, en apariencia, de la geometría no euclídea,¹ (por ejemplo, formas no rectilíneas) que se emplean para distorsionar y dislocar algunos de los principios elementales de la arquitectura como la estructura y la envolvente del edificio. (W)

Guangzhou Opera House © Zaha Hadid Architects

 



Guangzhou Opera House © Zaha Hadid Architects from Zaha Hadid Architects on Vimeo.

Fantasía geométrica de Zaha Hadid

Premios

Clasificación de los Sistemas de Representación

La representación de los objetos técnicos se realiza mediante una o varias imágenes que se determinan proyectando los objetos sobre un plano imaginario.

El sistema de representación queda definido por tanto por la posición de dicho plano y la del centro de proyección.

La posición del objeto respecto del plano y del centro puede variar la representación del mismo, determinando la convergencia en la proyección, en mayor o menor mediada, de las líneas que son paralelas en el espacio.

El dibujo técnico es un sistema de representación gráfica de diversos tipos de objetos, con el propósito de proporcionar información suficiente para facilitar su análisis, ayudar a elaborar su diseño y posibilitar la futura construcción y mantenimiento del mismo.(W)

Indeterminación de la proyección

La proyección de un elemento geométrico puede superponerse con la de otros elementos situados en una posición diferente en el espacio.

[caption id="attachment_14435" align="alignleft" width="212"] Indeterminación de la proyección[/caption]

Veamos primero el caso correspondiente a la proyección del elemento punto.
Al proyectar un punto (P) desde un centro de proyección (V) propio o impropio, la proyección P de dicho punto coincide con la de los puntos que se encuentran en el rayo proyectante de (P)

Una proyección sobre un único plano no permite restituir la información espacial de las coordenadas de los puntos proyectados. Se ha pasado de un sistema de tres coordenadas a uno de dos en el que se ha perdido por tanto parte de la información de posición de los elementos.

[caption id="attachment_14436" align="alignleft" width="213"] Indeterminación en rectas[/caption]

Al proyectar una recta (r) desde un centro de proyección (V) propio o impropio, la proyección r de dicha recta coincide con la de las rectas que se encuentran en el plano proyectante de (P). 

En ambos caos, proyección de la recta o del punto, la representación del elemento reduce la información espacial del mismo.

Cada sistema de representación soluciona esta indeterminación, imposibilidad de restituir la información tridimensional, de una forma diferente, haciéndolo más o menos adecuado a un uso técnico específico.

Soluciones a la indeterminación

La solución consiste en ampliar el número de proyecciones para determinar los elementos geométricos, o añadir datos alfanuméricos que las complementen.

1. Una proyección sobre un plano junto con información numérica


2. Dos proyecciones diferentes

• sobre un mismo plano


• sobre diferentes planos, uno de los cuales se abate, proyecta o superpone con el otro

Clasificación

Los sistemas de representación pueden clasificarse según diferentes criterios. Normalmente se ha admitido una clasificación recogiendo los más utilizados y que es la siguiente:

• Sistema diédrico


• Perspectiva axonométrica


• Perspectiva caballera


• Planos acotados


• Perspectiva cónica, lineal o sistema central

Esta clasificación puede estar planteada en base a las posibles aplicaciones de las mismas. Una “perspectiva” intuitivamente la asociamos con una representación tridimensional similar a una fotografía, en la que los volúmenes pueden interpretarse de forma natural. El sistema diédrico con diferentes vistas es un modelo más técnico fundamentalmente de uso industrial.

Tipos de proyección

Atendiendo al criterio de clasificación de la conservación de la razón simple, según los conceptos proyectivos, se puede realizar una clasificación que permite establecer modelos operativos similares.

Cónica	Cilíndrica
	Ortogonal	Oblícua

En todas las proyecciones se conserva la razón doble. Las proyecciones de tipo cilíndrico conservan además la razón simple, pudiendo tener una dirección de proyección ortogonal u oblicua respecto del plano de proyección. La dirección de proyección oblicua incide especialmente en la forma en que se puede medir en la perspectiva.

[caption id="attachment_13573" align="aligncenter" width="400"] Sistemas_de_representacion[/caption]

Geometría métrica : Inversión : Aplicación a la resolución de problemas de tangencias y angulares

La inversión es una transformación que permite resolver problemas con condiciones angulares.

Su aplicación puede ser directa o servir para reducir los problemas tratados a otros más sencillos de naturaleza conocida.

Los diferentes enfoques con los que podemos tratar un problema serán objeto de estudio mediante el desarrollo de un clásico y sencillo problema de tangencias.

La generalización de las ideas tratadas a otras formas de enunciado, en problemas similares de la misma naturaleza, será un ejercicio que permitirá al lector sistematizar los modelos de resolución.

Planteamiento del problema a estudiar

Supongamos el siguiente problema:

Determinar las circunferencias que son tangentes a una circunferencia y a una recta en uno de sus puntos.

[caption id="attachment_14017" align="aligncenter" width="387" caption="Enunciado del problema de tangencias con condición de punto de paso"][/caption]

El problema puede ser un caso particular de angularidad, en particular de isogonalidad (igual ángulo), respecto de dos circunferencias y una condición de paso. Tres aspectos simplifican este caso sin restar generalidad:

• El ángulo puede ser considerado nulo (condición de tangencias).


• Una de las circunferencias es una recta (radio infinito)


• El punto de paso se encuentra sobre uno de los elementos (Punto de tangencia T)

Estas singularidades suelen simplificar el trazado (número de líneas necesarias para la resolución) aunque los conceptos utilizados sean los mismos. La utilidad en un problema didáctico es precisamente esa simplificación ya que permite enfocar los conceptos con menor dificultad.

Este problema se podría enunciar de forma general como:

Determinar la circunferencia que forma angulos alfa y beta con dos circunferencias dadas y pasan por un punto P.

Resolveremos como modelo de análisis el primer caso haciendo posteriormente los comentarios necesarios para que el lector pueda abordar el caso genérico y, en consecuencia, toda la diversidad de casos derivados.

Enfoque primero: Simplificación de la solución buscada

Abordaremos en primer lugar el problema mediante el enfoque menos conceptual y más laborioso desde el punto de vista de los trazados gráficos necesario. Este modelo será de aplicación siempre que se disponga de un punto de paso como condición o restricción geométrica para el problema, no permitiendo la generalización para el caso de tres circunferencias. Es por tanto un enfoque incompleto aunque de gran aplicación en numerosos problemas.

Aplicaremos la inversión al conjunto de datos, resolveremos el problema con los datos transformados y deshaciendo la transformación ( la solución obtenida en el conjunto invertido) determinaremos  la solución buscada.

En este modelo de solución usaremos el punto de paso como centro de inversión. Al hacer esto y transformar los datos la solución que buscamos se convertirá en un elemento geométrico más sencillo (una recta), simplificando en gran parte el problema.

La idea principal es por tanto simplificar la solución a buscar

El valor de la potencia puede ser cualquiera, incluidos los que transformen algún elemento en él mismo con objeto de simplificar trazados. En un primer nivel de análisis evitaremos estos valores  particulares de la potencia de inversión para diferenciar claramente el conjunto original y el transformado.

[caption id="attachment_14033" align="aligncenter" width="409" caption="Inversión de centro el punto de paso T"][/caption]

Los punto P y Q de corte con la circunferencia de autoinversión elegida son dobles. La circunferencia transformada será tangente a las tangentes t1 y t2 desde el centro de inversión a la circunferencia, como vimos al estudiar la inversión en el plano.

Tomando como potencia de inversión la potencia del punto T respecto de la circunferencia c, ésta se convierte en una circunferencia doble (ortogonal a la de autoinversión).

La recta r es inversa de sí misma, ya que pasa por el centro de inversión.

Como la circunferencia buscada pasa por el punto T que hemos tomado como centro de inversión, su transformada será una recta que no pasa por dicho punto, y que cumplirá las respectivas condiciones angulares (tangencia) respecto de las inversas de la circunferencia c y la recta r ( será tangente a c' y  a r' ).

La condición de tangencia entre dos rectas se traduce en condición de paralelismo entre ellas.

En la figura se han obtenido las transformadas de las soluciones, tal y como se ha descrito.

[caption id="attachment_14034" align="aligncenter" width="389" caption="Soluciones transformadas"][/caption]

Las rectas s'1 y s'2 se convertirán en las soluciones al problema al deshacer la transformación. Los puntos de tangencia de estas rectas se convertirán en los de tangencia de dichas soluciones.

[caption id="attachment_14035" align="aligncenter" width="423" caption="Soluciones del problema al deshacer la inversión"][/caption]

Si en lugar de tener condiciones de tangencia tuviéramos condiciones angulares, las rectas tangentes s'1 y s'2 lo serían a las circunferencias goniómetras que determinamos al estudiar los problemas de rectas con condiciones angulares.

Enfoque segundo: Inversión de un dato en otro

Este enfoque es el más generalista, permitiendo reducir los problemas más complejos al problema fundamental de tangencias para el caso recta o circunferencia, o bien obtener relaciones entre los elementos que lo simplifiquen.

Podemos utilizar dos centros de inversión que relacionan a la recta r y la circunferencia c ( o a dos circunferencias). Un centro positivo I+, y otro que tendrá potencia negativa, I-. En este caso de análisis deben encontrase sobre la circunferencia c.

El punto de tangencia T se transformará en T' mediante la inversión de potencia positiva y en T'' con la inversión de potencia negativa, dando lugar cada uno de ellos a una de las soluciones buscada.

[caption id="attachment_14039" align="aligncenter" width="374" caption="Inversión de un dato en otro"][/caption]

En estas condiciones cualquier elemento tangente a la circunferencia c se convertirá en uno tangente a su transformada, la recta r=c'. Las soluciones serán por tanto circunferencias dobles, inversas de sí mismas, que pasarán por los puntos T y T' y serán ortogonales a la de autoinversión (no representada)

[caption id="attachment_14042" align="aligncenter" width="381" caption="Solución mediante la inversión de un dato en otro"][/caption]

Las soluciones se determinarán al encontrarse sus centros en la perpendicular a la recta por el punto de tangencia, en la mediatriz de TT' o alineados con el centro de la circunferencia dato y su punto de tangencia.

En otro artículo generalizaremos el caso de angularidad genérica; veremos que la condición de ortogonalidad a la circunferencia de autoinversión permite reducir a haces de circunferencias las familias de soluciones.

Este enfoque de la inversión de un dato en otro será la base para la sustitución de condiciones angulares por condiciones de ortogonalidad.

Geometría métrica

Geometría métrica : Inversión en el plano

La inversión es una transformacion homográfica que conserva las relaciones angulares (es conforme).

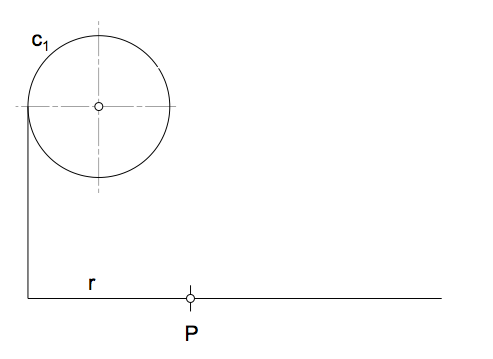
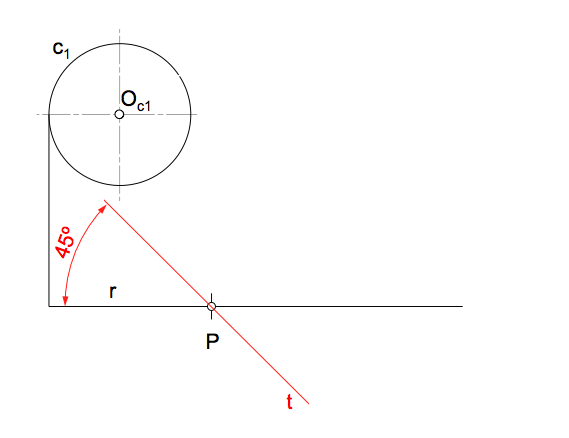
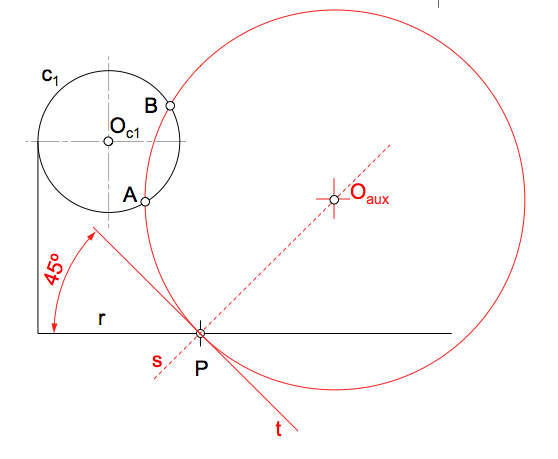
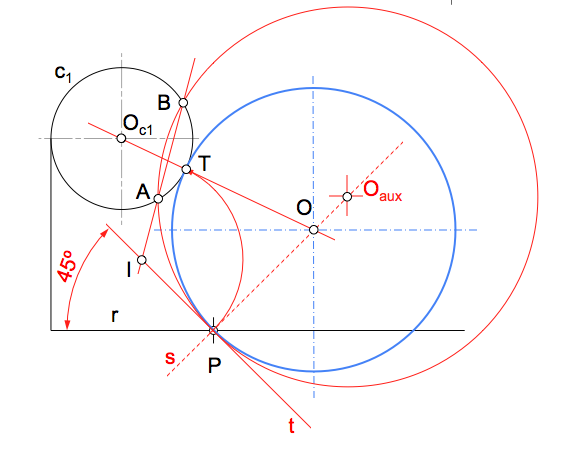
Su principal aplicación en geometría es la determinación de problemas con condiciones angulares entre los que se encuentran la resolución de ejercicios con tangencias.

Se basa en los conceptos de potencia; es una transformación involutiva que puede tener elementos dobles en los casos de potencia positiva.

Definición de la transformación

La inversión es una transformación con centro. Esto significa que un punto y su transformado se encuentran alineados con el centro de inversión, de forma análoga a la transformación conocida como homotecia.

La relación entre las posiciones relativas de cada punto y su transformado respecto del centro de inversión se basan en el concepto de potencia.

Dado un centro "I", y un par de puntos inversos "P" y "P'", el producto de las distancias de estos puntos al centro de inversión es constante y se denomina potencia de inversión.

IP * IP' = IQ * IQ' = K*K = $latex K^2$

Si la potencia de inversión es positiva, un punto y su transformado se encuentran al mismo lado respecto del centro de inversión. Los puntos que se encuentran a distancia K del centro son dobles. La circunferencia de radio la raíz de la potencia, valor K, es doble y de puntos dobles, denominándose circunferencia de autoinversión.

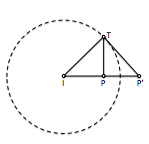
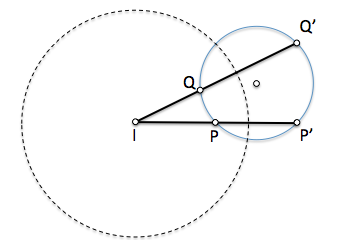
[caption id="attachment_13960" align="aligncenter" width="341" caption="Dos puntos y sus inversos son concíclicos"][/caption]

Si la potencia es negativa el centro de inversión se encuentra entre cada punto y su transformado. La circunferencia de autoinversión es doble pero no de puntos dobles.

Inversión de elementos

Estudiaremos la inversión de puntos junto con cuatro posibles casos de transformación, dos para la recta y otros dos para la circunferencia, en los que el centro de inversión puede encontrarse en cualquier posición respecto del elemento geométrico o bien situado sobre él.

• Rectas que contienen al centro de inversión


• Rectas que no contienen al centro de inversión


• Circunferencias que contienen al centro de inversión


• Circunferencias que no contienen al centro de inversión

Inversión de Puntos

La inversión de puntos se puede resolver mediante construcciones de potencia o con los denominados teoremas del cateto y de la altura.

Inversión de potencia positiva

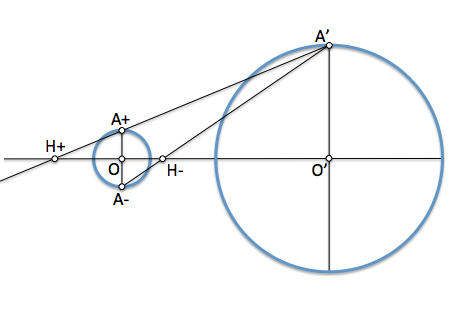
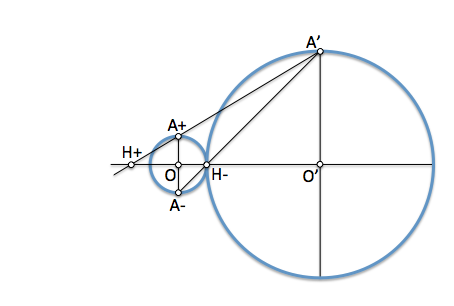
En este caso uno de los puntos es interior a la circunferencia de autoinversión y el otro exterior ( o son dobles y están sobre ella), pero al mismo lado respecto de I. Podemos aplicar el teorema del cateto haciendo uso de la circunferencia de autoinversión tal y como se aprecia en la figura.

[caption id="attachment_13982" align="aligncenter" width="353" caption="Inversión positiva"][/caption]

Los conceptos de potencia nos permiten asegurar que dos puntos y sus inversos son concíclicos (están en una misma circunferencia que es doble en la inversión y corta ortogonalmente a la misma).

Inversión de potencia negativa

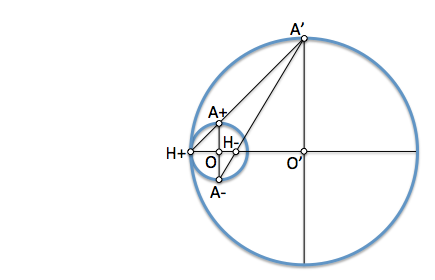
Una inversión negativa se puede obtener mediante una positiva de igual potencia (en módulo) mas una simetría central. Aplicando el teorema de la altura determinaremos pares de puntos inversos.

[caption id="attachment_13983" align="aligncenter" width="395" caption="Inversión negativa"][/caption]

 Los puntos diametrales de la circunferencia de autoinversión son inversos.

Inversión de rectas que contienen al centro de inversión

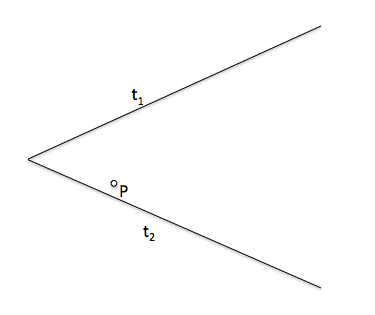
Este caso es el más sencillo ya que, por la definición de la transformación, el inverso de cada punto se encuentra alineado con este punto y con el centro de inversión y en consecuencia la inversa de la recta, si contiene al centro de inversión, es la propia recta.

[caption id="attachment_13985" align="aligncenter" width="493" caption="Inversión de una recta"][/caption]

Inversión de rectas que no contienen al centro de inversión

Inversión de circunferencias que contienen al centro de inversión

Estos dos casos se pueden estudiar conjuntamente ya que la transformación es involutiva y, como veremos, la invesa de una recta que no contiene al centro de inversión es una circunferencia que lo contiene y viceversa.

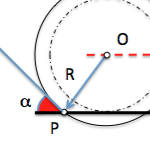
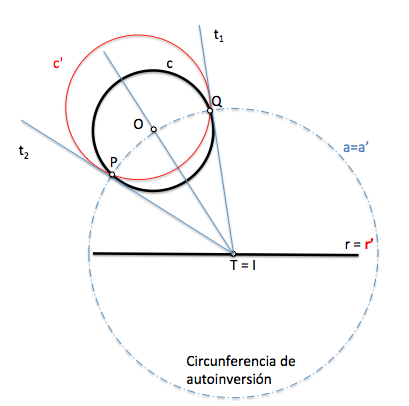
Como dos puntos y sus inversos son concíclicos las rectas que unen dos puntos y la que unen sus inversos son antiparalelas de las rectas soportes que unen cada punto y su inverso (dos a dos forman el mismo ángulo). En la figura la recta PQ forma un ángulo alfa con la recta QQ' idéntico al que forma la recta P'Q' con PP'.

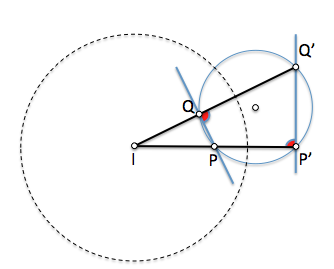
[caption id="attachment_14007" align="aligncenter" width="334" caption="Antiparalelismo"][/caption]

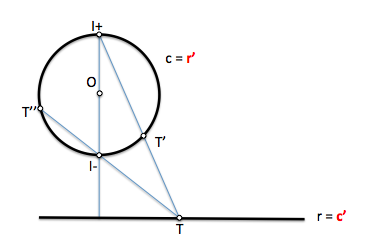
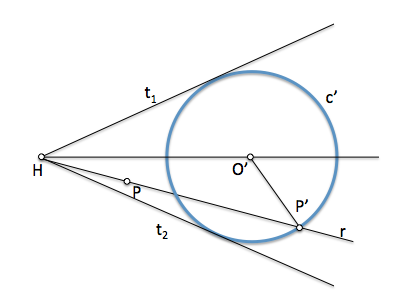
Al invertir una circunferencia que pasa por el centro de inversión y un punto P, su inversa pasará por el transformado P'. Si invertimos otro punto Q en Q' vemos que el ángulo en Q reflejado en la figura debe ser recto por ser inscrito en una semicircunferencia. En consecuencia el segmento P'Q' debe formar un ángulo recto con la recta PP' y está obligado a estar en la recta c'. Repitiendo esta operación para los infinitos puntos de la circunferencia obtendremos la recta c'

[caption id="attachment_13953" align="aligncenter" width="400" caption="Inversión de recta en circunferencia"][/caption]

En consecuencia:

La inversa de una circunferencia que pasa por el centro de inversión es una recta que no pasa, de dirección perpendicular al diámetro que contiene al centro de inversión.

Como la transformación es involutiva:

La inversa de una recta que no pasa por el centro de inversión es una circunferencia con centro en la perpendicular desde el centro de inversión a dicha recta.

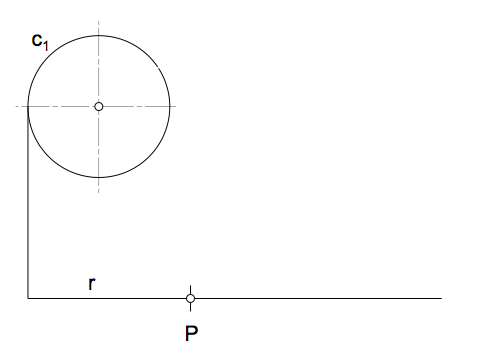
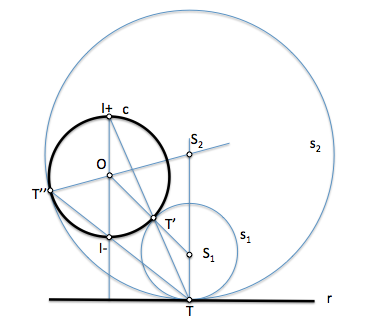
Inversión de circunferencias que no contienen al centro de inversión

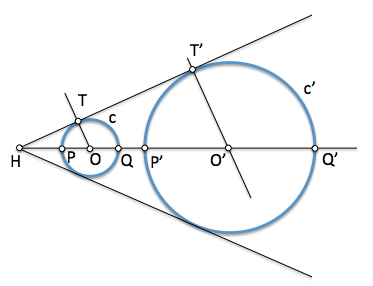
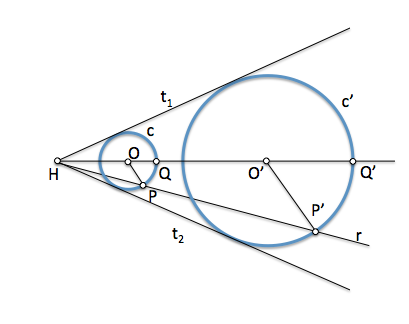
Al estudiar la transformación mediante homotecia hemos visto que dos circunferencias coplanarias se pueden relacionar mediante dos centros diferentes. En la figura se ha representado el centro I que establece una homotecia de razón postiva en la que T y T' son homólogos, igual que P y Q' o bien Q y P'. La razón de homotecia es por tanto:

IT / IT' = IP / IQ' = IQ / IP' = Kh

Por otro lado, la potencia del punto I respecto de la circunferencia c es:

W = IP * IQ

Dividiendo la potencia por la razón de homotecia:

W / Kh = IQ * IQ' = cte

Vemos que las dos circunferencias son inversas con centro I y potencia W / Kh

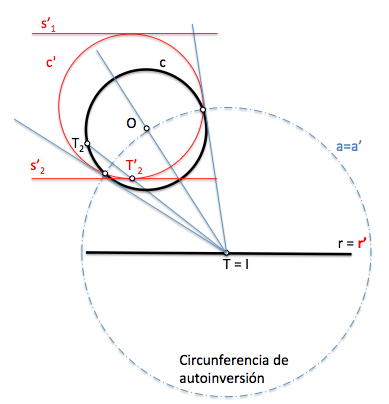
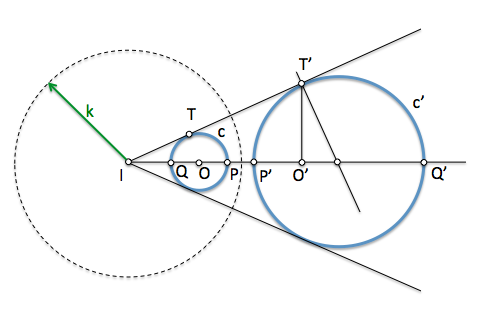
[caption id="attachment_13981" align="aligncenter" width="484" caption="Inversa de una circunferencia"][/caption]

Por lo tanto:

La inversa de una circunferencia que no pasa por el centro de inversión es otra circunferencia, siendo el centro de inversión el centro de homotecia que las relaciona.

Cuando el centro de homotecia es exterior a las circunferencias el valor de la potencia es  positivo, por lo que el signo de la potencia de inversión se corresponde con el de los centros de homotecia. Sin embargo, si el centro de homotecia es interior a las circunferencias, el signo se invierte.

Cuando el centro de homotecia se encuentra en la circunferencia, al ser la potencia nula, no se puede considerar que sea de inversión.

Nótese que aunque los centros de las circunferencias son homólogos, no son inversos.

El inverso O' del centro O de una circunferencia c que no pasa por el centro de inversión es el pie de la polar del centro de inversión respecto de la circunferencia inversa c'.

Conformidad de la transformación

Una transformación es conforme si el ángulo que forman dos elementos es el mismo que el que forman los elementos transformados. La inversión es una transformación conforme por lo que es de gran utilidad en la resolución de problemas con condiciones angulares.

El antiparalelismo entre las rectas que unen dos puntos y sus inversos, respecto de las que unen cada uno de ellos con su inverso es la base de la demostración.

[caption id="attachment_13958" align="aligncenter" width="336" caption="Las rectas que unen cuatro puntos de una circunferencia, dos a dos son antiparalelas"][/caption]

Supongamos una curva c que pasa por dos punto P y Q. El segmento PQ es una cuerda de esta curva. En el límite, cuando hacemos coincidir los puntos P y Q, la cuerda se convierte en la tangente a la curva por lo que:

El ángulo que forma la tangente a una curva en un punto P con la recta que contiene al punto y su inverso, es el mismo que el que forma la tangente a la curva inversa.

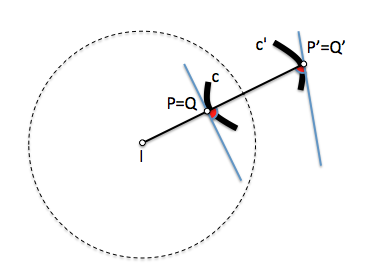
[caption id="attachment_13957" align="aligncenter" width="370" caption="Una curva y su inversa forman el mismo ángulo con la recta que une cada par de puntos inversos"][/caption]

Si aplicamos a dos curvas, al conservarse respectivamente el ángulo que forman sus tangentes concluimos que:

El ángulo que forman dos curvas es el mismo que el formado por sus curvas inversas, por lo que la inversión es una transformación conforme.

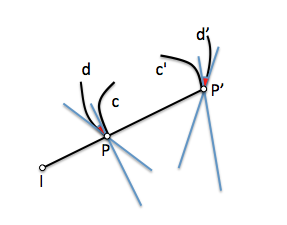
[caption id="attachment_13956" align="aligncenter" width="287" caption="Conformidad en la inversion"][/caption]

La aplicación a la resolución de problemas puede hacerse de dos formas conceptualmente diferentes:

• Simplificando los datos del problema.


• Simplificando la solución buscada.

Veremos en una nueva entrada una discusión en profundidad sobre estos dos modelos de análisis, aplicándolos a un problema de angularidad.

Geometría métrica

Enlaces externos

• Inversión en el plano (W)


• Propiedades de la inversión (applet interactivo en gaussianos)

Geometría métrica : Homotecia

[caption id="attachment_14001" align="alignleft" width="150" caption="Transformaciones - homotecia"][/caption]

La homotecia es una transformacion homográfica que conserva las relaciones de medida entre cada par de segmentos homotéticos u homólogos.

Conserva el paralelismo entre una línea y su transformada,  por lo que determina figuras semejantes y mantiene las relaciones angulares (es conforme).

Su principal aplicación en geometría es la determinación de problemas con relaciones de áreas en figuras semejantes; también es de utilidad para la resolución de algunos ejercicios de tangencias.

Dos figuras semejantes tienen la misma forma y diferente área

[caption id="attachment_13991" align="aligncenter" width="240" caption="Homotecia"][/caption]

Se basa en los conceptos de semejanza que vimos en el teorema de Thales; no es una transformación involutiva y no puede tener elementos dobles salvo el centro. Pertenece al grupo de las transformaciones afines.

Definición de la transformación

La homotecia es una transformación con centro. Esto significa que un punto y su transformado se encuentran alineados con el centro de homotecia o semejanza, de forma análoga a la transformación conocida como inversión que se verá posteriormente.

La relación entre las posiciones relativas de cada punto y su transformado respecto del centro de homotecia se basan en el concepto de semejanza.

Dado un centro "H", y un par de puntos homólogos "P" y "P'", el cociente de las distancias de estos puntos al centro de homotecia es constante y se denomina razón de homotecia.

HP / HP' = HQ / HQ' = HT / HT' = K

[caption id="attachment_13989" align="aligncenter" width="373" caption="Circunferencias homotéticas"][/caption]

Centros de homotecia entre dos circunferencias

Relacionar mediante esta transformación dos circunferencias es de especial interés para su aplicación en los problemas de tangencias, así como para el posterior estudio de otra transformación: la inversión.

Si suponemos que dos circunferencias son homotéticas, los puntos situados sobre radios paralelos deben ser homólogos. Dependiendo del sentido del radio tendremos transformaciones de razón positiva (los dos radios en el mismo sentido) o negativa (diferente sentido). Los centros positivo, H+, y negativo, H-, deben encontrarse sobre las rectas que unen cada par de puntos homólogos (A-A') así como en la línea que une los centros de las circunferencias ya que también son homotéticos.

[caption id="attachment_13992" align="aligncenter" width="460" caption="Centros de homotecia de dos circunferencias 1"][/caption]

Podemos ver como en algunas posiciones particulares alguno de los centros de homotecia puede estar situado sobre las propias circunferencias, como es el caso en el que éstas son tangentes entre sí.

[caption id="attachment_13993" align="aligncenter" width="454" caption="Centros de homotecia de dos circunferencias 2"][/caption]

Si una es interior a la otra veremos además que el otro centro de homotecia es interior a ambas circunferencis.

[caption id="attachment_13994" align="aligncenter" width="435" caption="Centros de homotecia de dos circunferencias 3"][/caption]

Aplicación de la homotecia a los problemas de tangencias

Una de las posibles aplicaciones de esta transformación es la determinación de circunferencias con condiciones de tangencia respecto de dos rectas.

Supongamos el siguiente ejercicio:

Determinar las circunferencias tangentes a dos rectas y que pasan por un punto P

[caption id="attachment_13997" align="aligncenter" width="375" caption="Homotecia - Problema de tangencias"][/caption]

Si suponemos que el punto de intersección de las rectas tangentes es un centro de homotecia, H, podemos convertir la circunferencia que buscamos con una razón cualquiera en otra circunferencia que debe ser tangente a dichas rectas. Para realizar esta transformación elegiremos un radio cualquiera para esta nueva circunferencia

[caption id="attachment_13998" align="aligncenter" width="402" caption="Homotecia - Problema de tangencias planteado"][/caption]

El punto P debe tener un punto homólogo, P', en la nueva circunferencia. Este punto se encontrará en la intersección de esta circunferencia auxiliar y la recta r que pasa por P y por el centro H de homotecia (Nótese que puede haber otro punto de intersección de r con c', válido para obtener una segunda solución).

[caption id="attachment_13999" align="aligncenter" width="409" caption="Homotecia - Problema de tangencias solucionado"][/caption]

El centro de la circunferencia solución lo determinamos obteniendo el radio homólogo del que pasa por P', que pasará por el punto P y será paralelo al anterior.

Geometría métrica