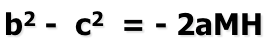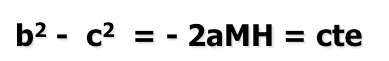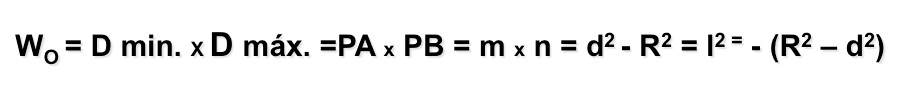Geometría métrica : Eje radical de dos circunferencias

Los lugares geométricos sirven para determinar la solución de problemas con restricciones geométricos.

Entre las condiciones más utilizadas se encuentran las de naturaleza angular y dentro de éstas las de ortogonalidad.

Dadas dos circunferencias coplanarias, el conjunto simplemente infinito de circunferencias que las cortan ortogonalmente se agrupan en un conjunto denominado haz de circunferencias corradicales; estas circunferencias tienen su centro en una recta denominada eje radical.

El eje radical de dos circunferencias es el lugar geométrico de los puntos del plano

• que son centros de circunferencias ortogonales a dichas circunferencias


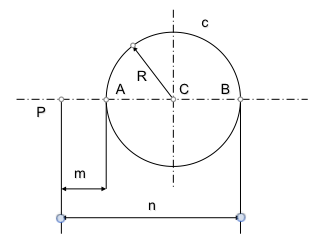
• que tienen igual potencia respecto a dichas circunferencias


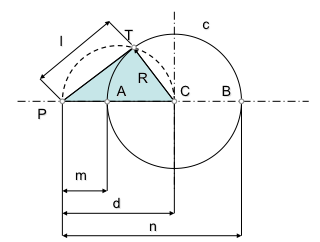
• desde los cuales se pueden trazar segmentos tangentes de igual longitud a las circunferencias

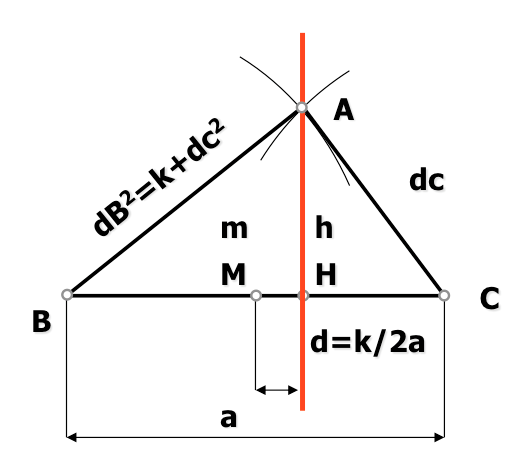
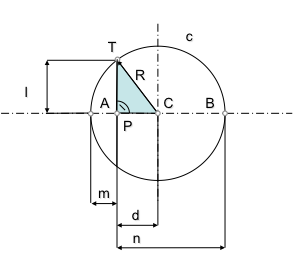
Para determinar este lugar geométrico, eje radical, nos apoyaremos en una figura de análisis compuesta por dos circunferencias que son cortadas ortogonalmente por la buscada.

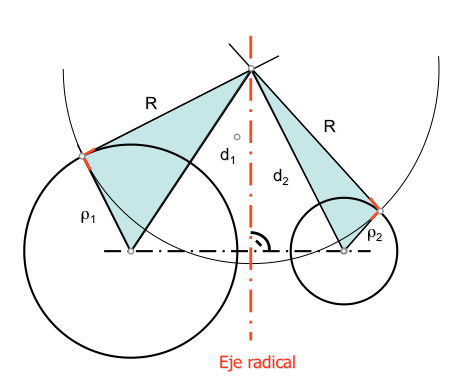
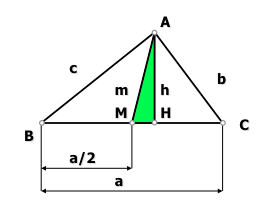
Vemos en los triángulos rectángulos que se cumple, aplicando pitágoras, las siguientes relaciones:



de donde podemos obtener



que como hemos visto al estudiar el lugar geométrico de la diferencia de cuadrados de distancias a dos puntos fijos, es una recta. Esta recta se denomina eje radical de las dos circunferencias.

Centro radical de tres circunferencias

Vemos que al imponer dos restricciones de ortogonalidad se determina un lugar geométrico para los centros de las soluciones que lo cumplen. Si introducimos una tercera condición obtendremos una solución única que podemos obtener mediante intersección de los lugares geométricos referidos.

El Centro radical CR de tres circunferencias coplanarias es un punto de su plano:

• es intersección de los tres ejes radicales de las circunferencias


• tiene igual potencia respecto a dichas circunferencias


• es centro de la circunferencia ortogonal a dichas circunferencias


• desde el  cual se pueden trazar segmentos tangentes de igual longitud a las tres circunferencias

El centro radical se puede obtener mediante la intersección de dos ejes radicales

[caption id="attachment_13726" align="aligncenter" width="475"] 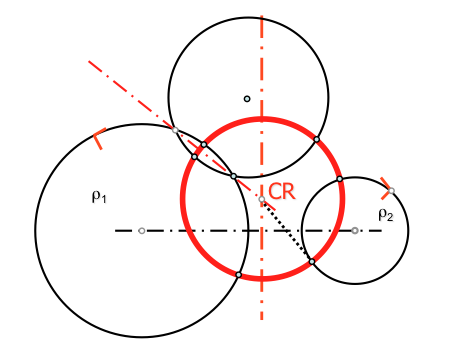Centro radical de tres circunferencias[/caption]

Geometría Métrica

Lugar Geométrico de la Suma/Diferencia de cuadrados de distancias a dos puntos fijos

Los lugares geométricos permiten determinar puntos que satisfacen una determinada condición geométrica. Son de interés en la resolución de problemas en los que se imponen restricciones métricas o geométricas.

Algunos lugares geométricos son elementales y sirven para definir figuras geométricas conocidas, mientras que otros exigen elaborados procesos de determinación.

Así, por ejemplo, el lugar geométrico de los puntos del plano cuya distancia a un punto fijo es constante es una circunferencia de centro el punto referido y de radio la distancia dada.

Relaciones en el triángulo

La aplicación directa del teorema de Pitágoras nos permite obtener algunos lugares geométricos de alto interés en el desarrollo de teoremas avanzados de la geometría métrica.

En la figura se tiene el triángulo ABC y se han obtenido, sobre el lado "a", el punto medio "M" y el pie de la altura "H" al determinar su altura "h" desde el vértice "A". Esto permite determinar tres triángulos rectángulos (un ángulo recto) que podemos relacionar entre sí para obtener dos importantes lugares geométricos.

Los triángulos a los que nos referimos son:

• AHB


• AHC


• AHM

Como se aprecia en la figura, los tres triángulos comparten el lado "AH" como uno de sus catetos, y el otro cateto se encuentra en el lado "a", base, del triángulo; Son triángulos rectángulos ya que el lado "AH" es la altura del triángulo y en consecuencia es perpendicular a dicha base.

Aplicando el teorema de pitágoras, podemos obtener las tres relaciones siguientes:

sumando las dos primeras tendremos la suma de dos cuadrados

mientras que si restamos una a la otra tendremos la diferencia de dos cuadrados

Lugar Geométrico de los puntos cuya  diferencia de cuadrados de distancias a dos puntos fijos es constante.

Veamos cómo podemos utilizar las relaciones anteriores para determinar el lugar geométrico de los puntos del plano que cumplen que la diferencia de los cuadrados de su distancia a dos puntos fijos es constante. Este teorema que vamos a determinar se puede enunciar de la siguiente forma:

El lugar geométrico de los puntos cuya diferencia de los cuadrados de las distancias a dos puntos fijos B y C es una cantidad constante k es una recta ortogonal a BC cuya distancia al punto medio de BC es d=K/2BC.

Supongamos que uno de los puntos del plano que cumple esa condición es el vértice "A" del triángulo ABC, y que los puntos fijos a los que nos referimos son "B" y "C".

De las relaciones anteriores podemos utilizar la que expresa la diferencia de cuadrados de distancias a los puntos "B" y "C", e imponer la condición de que esta relación permanezca constante.

Al ser fija la distancia entre los puntos "B" y "C", el valor del lado “a” es constante. Para que la igualdad que expresa la ecuación sea constante la distancia “MH” tiene que serlo también ya que "a" no varía y "2" es un número que tampoco cambia.

Vemos que el segmento “MH” es la proyección de la mediana "m" (recta que une un vértice con el punto medio "M" del lado opuesto) sobre el segmento “BC”

Esto implica que el punto "A" puede estar en cualquier posición del plano de forma  que la proyección de la mediana sobre “BC” permanezca constante; el punto “A” tiene que moverse por lo tanto sobre la recta “h”, por lo que el lugar geométrico buscado debe de ser esa recta.

Este lugar geométrico permitirá determinar el "eje radical" de dos circunferencias como se verá en el estudio de ortogonalidad.

Lugar Geométrico de los puntos cuya  suma de cuadrados de distancias a dos puntos fijos es constante.

De la expresión obtenida para la suma de cuadrados:



se deduce que, al ser "a" constante, para que la expresión lo sea, debe  de ser el valor "m" de la mediana también un valor fijo, con lo que se concluye que el lugar geométrico debe de ser una circunferencia de radio dicho valor de la mediana.

Geometría Métrica

SmartInversion : Caleidociclo volador robotizado

SmartInversion es un ingenio, de la empresa Festo,  capaz de impulsarse en el aire gracias a un movimiento denominado inversión en el que una banda formada por poliedros (tetraedros) ligeros articulados, rellenos de helio, giran sobre ellos mismos. Este movimiento constante, rítmico pulsante, es el que le da la propulsión en el medio.

En es siguiente video se puede ver este novedoso concepto en una interesante animación de carácter didáctico, mientras que en el segundo tenemos una "demo" de vuelo real.

SmartInversion is a helium-filled flying object that moves through the air by turning inside-out. This constant, rhythmically pulsating movement is known as inversion and gives the flight model its name. With the intelligent combination of extreme lightweight construction, electric drive units and control and regulation technology, inversion kinematics can be indefinitely maintained to produce motion through the air.

¿Un "Kaleidocycle" volador?

 

SmartInversion web de Festo
Flying object propels itself by flipping inside out New Scientific TV

SmartInversion: el robot que vuela modificando su propia geometría para impulsarse (Microsiervos)

Transformaciones geométricas : Homografías Vs Correlaciones

Las transformaciones geométricas pueden entenderse como el conjunto de las operaciones geométricas que permiten crear una nueva figura a partir de una previamente dada, así como las propiedades invariantes que se obtienen en ellas.  La nueva figura se llamará "homóloga" o correlativa de la original dependiendo de la naturaleza de la transformación de sus elementos básicos.

Una homografía es una transformación que conserva la naturaleza de los elementos transformados.

• Un punto se transforma en otro punto


• Una recta se transforma en otra recta


• Un plano se transforma en otro plano

Una correlación es una transformación que NO conserva la naturaleza de los elementos transformados.

• Un punto se puede transformar en una recta o plano, pero no en otro punto


• Una recta se puede transformar en un punto o plano, pero no en otra recta


• Un plano se puede transformar en una recta o punto, pero no en otro plano

En la figura anterior se esquematizan estos conceptos. Un determinado elemento, por ejemplo un punto, se transforma en otro elemento de igual naturaleza, punto, mediante una homografía, mientras que si realizamos una correlación su transformado podrá ser una recta o un plano pero nunca un punto.

Metodología de análisis de una transformación geométrica

Cuando estudiamos una transformación geométrica debemos analizar sistemáticamente una serie de apartados que nos darán un conocimiento suficiente de la misma.

• Definición de la transformación


• Transformación de elementos básicos


• ¿Mantiene la forma? (es Semejante)


• ¿Conserva los ángulos (es Conforme )?


• ¿Es involutiva?


• Propiedades


• Aplicaciones principales

La definición de la transformación deberá incluir el análisis del número de parámetros o restricciones necesarios para su correcta determinación, Así, una traslación deberá definirse mediante una dirección y un módulo o valor para indicar la distancia entre dos puntos homólogos o transformados, pero también quedará definida mediante la determinación de un punto y el transformado. Vemos que la misma transformación puede determinarse por tanto con datos diferentes.

Analizaremos cómo obtener los transformados de cada uno de los elementos básicos: puntos, rectas, circunferencias .... ya que una figura geométrica se puede descomponer en dichos elementos para ser transformada.

Los invariantes o aspectos métricos y proyectivos que se mantienen en la transformación servirán para simplificar la utilización de las operaciones necesarias en la transformación, así como para determinar sus posibles aplicaciones en la resolución de problemas geométricos.

En particular es de especial interés saber el comportamiento de las relaciones angulares; si una recta y su transformada son paralelas y si el ángulo que forman dos elementos se mantiene en la transformación (transformaciones conformes).

En particular en el caso de las homografías es interesante determinar si la transformación es involutiva, es decir, si al aplicar la transformación al transformado de un elemento se obtiene el elemento original. Por ejemplo una traslación no es involutiva, ya que al aplicar el movimiento al transformado de un punto se obtiene un punto diferente, mientras que una simetría si es involutiva. (No se debe confundir la involución con la transformación inversa).

Geometría métrica

Geometría métrica : Concepto de "Potencia de un punto respecto de una circunferencia"

El concepto de potencia de un punto respecto de una circunferencia permite relacionar las nociones estudiadas en los teorema de Thales y Pitágoras y es la puerta para el estudio de los problemas de tangencias y transformaciones como la inversión.

Usaremos los conceptos de arco capaz sobre un segmento en nuestras demostraciones, por lo que se sugiere su repaso.

Este concepto se basa en el producto de dos segmentos y, como veremos mas adelante, permite determinar algunos lugares geométricos de gran importancia como por ejemplo el eje radical de dos circunferencias.

Definición de potencia

La primera definición de potencia se basa en determinar la máxima y mínima distancia a una circunferencia y obtener su producto métrico.

La potencia W de un punto P respecto de una circunferencia c es el producto de la mayor por la menor distancia del punto P a la circunferencia c.

[caption id="attachment_13662" align="aligncenter" width="321" caption="Potencia de un punto respecto de una circunferencia"][/caption]

En la figura vemos que la potencia del punto P respecto de la circunferencia es el producto de los segmentos "m" y "n", mínima y máxima distancia desde el punto a la circunferencia. Estos segmentos se encuentran en el diámetro de la circunferencia que contiene al punto P.

Relaciones métricas de la Potencia

Podemos relacionar métricamente el concepto básico de potencia respecto de una circunferencia, mediante el teorema de pitágoras, con el segmento de tangencia que se obtiene desde el punto a la circunferencia.

La Potencia de un punto P respecto de una circunferencia es igual a la diferencia de cuadrados entre la distancia del punto P al centro C de la circunferencia y el radio R de la misma; también al cuadrado del segmento PT de tangente si P es exterior.

 Si tenemos en cuenta que el segmento "m" es igual a la distancia "d" del punto "P" al centro "C" de la circunferencia "c", menos el radio "R" de la misma (d-R), y que el segmento "n" es la suma de "d" y "R" (d+R) tendremos que:

Como la suma de dos variables multiplicada por la diferencia es la diferencia de sus cuadrados, vemos que la potencia "W" es igual a la diferencia de los cuadrados de la distancia "d" y del radio "R" de la circunferencia. Esta expresión nos recuerda al cateto de un triángulo rectángulo, cuyo cuadrado es igual a la diferencia de cuadrados de la hipotenusa y del otro cateto (lado l).

Si el punto P es interior a la circunferencia no existirá el segmento de tangencia, pero podemos establecer igualmente la relación con los lados de un triángulo pitagórico.

La Potencia de un punto P respecto de una circunferencia es igual a la diferencia de cuadrados de la distancia del punto P al centro C de la circunferencia y el radio R de la misma y también al cuadrado del segmento  de semicuerda PT perpendicular a PC si P es interior.

Potencia de un punto (Wikipedia)

 Geometría métrica

Sistemas de representación : Incidencia (Intersecciones) [ Geometría descriptiva ]

Los problemas de incidencia tratan de determinar los elementos comunes a dos figuras geométricas; se pueden definir como casos especiales de pertenencia. Son independientes de la métrica del sistema de representación y se pueden resolver mediante modelos generalizables en todos ellos.

Partiendo de los elementos geométricos fundamentales  recta y plano, podemos aplicar los conceptos de dualidad para analizar los posibles problemas que se pueden presentar.

• Seccionar una recta por un plano es definir el punto que pertenece a ambos elementos


• Seccionar una recta por otra recta es definir el punto que pertenece a ambos elementos


• Seccionar un plano por otro plano es definir la recta que pertenece a ambos elementos


• Seccionar un plano por una recta es definir el punto que pertenece a ambos elementos

En general estos problemas se resolverán mediante planos auxiliares que elegiremos convenientemente como se verá posteriormente.

Como conceptos generales de aplicación en los diferentes casos de determinación de intersecciones, podemos enunciar que:

• La intersección de dos planos tiene la dirección común a ambos planos


• Tres planos se cortan en un punto


• Al seccionar a un plano por planos paralelos se determinan rectas paralelas entre sí.


• Una recta y su proyección sobre un plano dado se cortan en el plano de proyección.

Intersección de recta y plano

Resolveremos en Sistema Diédrico este problema sin restar generalidad en el modelo de resolución. Los conceptos espaciales son idénticos, así como los trazados derivados.

El haz de planos de base una recta (r) secciona a un plano π según un haz de rectas de vértice el punto (I) de intersección de (r) y el plano π.

[caption id="attachment_13535" align="aligncenter" width="358" caption="Intersección de recta y plano"][/caption]

Para determinar la intersección de un plano (α) y una recta (r) se utiliza un plano (β) auxiliar que contenga a la recta. La intersección (i) entre los planos contiene al punto (I) buscado

El plano auxiliar se elegirá de forma que sea proyectante sobre el plano de proyección. Esto significa que contiene a la dirección de proyección y en consecuencia se representará como una línea recta. En diédrico además se cumplirá que, al ser la dirección de proyección normal al plano, el plano será perpendicular al de proyección.

[caption id="attachment_13536" align="aligncenter" width="327" caption="Intersección de recta y plano"][/caption]

Supongamos el siguiente ejemplo en el que se pretende obtener la intersección que produce una recta en un plano definido por dos rectas que se cortan.

[caption id="attachment_13537" align="aligncenter" width="356" caption="Ejemplo: Intersección de recta y plano definido por dos rectas"][/caption]

• Las rectas (r) y (s) pasan por el punto (P) y determinan un plano (α).


• La recta (a) corta a dicho plano en el punto (I) que es el que queremos determinar en las proyecciones diédricas.

El plano (β) contiene a la recta (a) siendo proyectante sobre la proyección vertical, y su intersección con el plano (α) determina la recta  i, (α∩β), que contiene al punto (I).

[caption id="attachment_13539" align="aligncenter" width="361" caption="Resolución : Intersección de recta y plano"][/caption]

Intersección de dos planos

Veamos primero un planteamiento espacial del problema que nos puede permitir reducir el problema al caso anterior de intersecciones.

Podemos realizar dos enfoques de este problema.

[caption id="attachment_13541" align="aligncenter" width="358" caption="Análisis de la Intersección de dos planos"][/caption]

• En primer lugar podemos utilizar dos planos auxiliares que seccionan a los planos alfa y beta en dos rectas cada uno. Estas rectas a su vez se cortan en dos punto (I1 e I2) que pertenecen a la intersección buscada.


• El segundo enfoque consiste en elegir dos rectas de uno de los planos y determinar los puntos de intersección que producen en el otro plano, tal y como se ha visto en el ejemplo de intersección de recta y plano.

En ambos casos la utilización de planos auxiliares forma parte de la metodología de resolución.

[caption id="attachment_13573" align="aligncenter" width="400" caption="Sistemas_de_representacion"][/caption]

Sistemas de representación : Relaciones perspectivas [ Geometría descriptiva ]

Hemos visto un modelo general que relacionas los diferentes tipos de proyecciones:

• Cónica


• Cilíndrica ortogonal


• Cilíndrica oblícua.

Veamos con un ejemplo aplicado las relaciones de Perspectividad en las proyecciones.

Dos proyecciones sobre un mismo plano de una recta (r), son perspectivas entre si, con centro perspectivo, sobre el plano de proyección, alineado con los respectivos centros de proyección.

En particular son de especial interés el caso de dos proyecciones cilíndricas y el caso en que se relacionan ambas.

[caption id="attachment_13482" align="aligncenter" width="506" caption="Relaciones perspectivas"][/caption]

Ejercício de ejemplo

El punto (A) del espacio se ha proyectado oblicuamente sobre el plano del dibujo Π según A1, ortogonalmente según A’’ y cónicamente desde (V) según A. El punto (V) se ha proyectado a su vez ortogonalmente sobre el plano del dibujo según V”. Este punto se encuentra a una distancia del plano Π igual al radio de la circunferencia representada, con centro en V”.
Se pide determinar el ángulo que forma la proyección oblicua con el plano de proyección.

[caption id="attachment_13483" align="aligncenter" width="522" caption="Ejemplo de aplicación de relaciones perspectivas"][/caption]

La figura de análisis nos permite observar una perspectiva libre del problema.

[caption id="attachment_13484" align="aligncenter" width="345" caption="Figura de análisis"][/caption]

Los triángulos rectángulos AVV” y (A)A”A1 permiten determinar la solución buscada.

Primero se puede construir AVV” ya que se conoce la distancia VV” que es igual al radio del círculo de distancias. El segundo triángulo rectángulo, (A)A”A1, viene determinado por sus catetos, A”A1 que es un dato dado en el problema y (A)A” que se obtiene en el paso anterior.

Se deja en manos del lector la resolución gráfica del problema como ejercício para fijar los conceptos.

[caption id="attachment_13573" align="aligncenter" width="400" caption="Sistemas_de_representacion"][/caption]