El problema del campo de fútbol

Un curioso problema, que suelo proponer en clase a mis alumnos, en el que podemos utilizar los conocimientos geométricos aprendidos al estudiar el concepto de potencia, es el de determinar la posición óptima de disparo a una portería de fútbol desde una trayectoria dada.

Podemos suponer que el jugador que realiza el disparo tiene suficiente potencia para poder realizarlo desde cualquiera de los puntos de su trayectoria, siendo por tanto el más adecuado aquél que le ofrezca mayor ángulo de visualización de la portería como veremos a continuación.

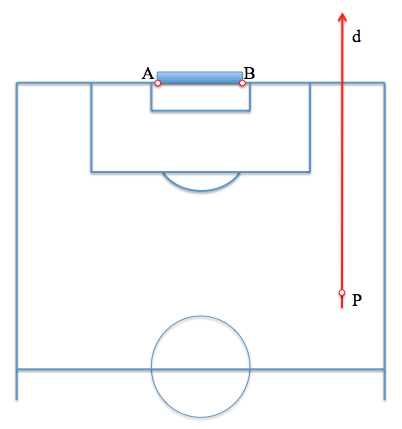
Para simplificar el enunciado, sin restar generalidad al problema, supondremos que el jugador se encuentra en un punto P del campo y corre paralelo a la banda (según la dirección d). La portería quedará determinada por el segmento AB.

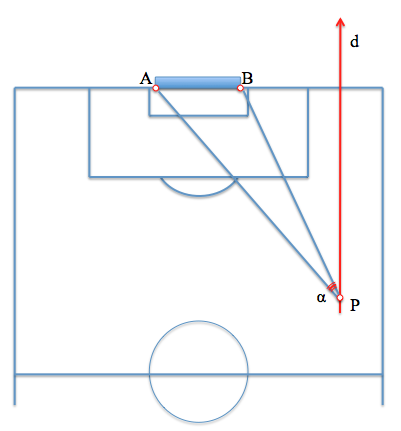
La posición del jugador le permitirá ver a la portería bajo un cierto ángulo "alfa". Nuestro problema será por lo tanto encontrar un nuevo punto de la trayectoria "d" desde el que este ángulo sea máximo.

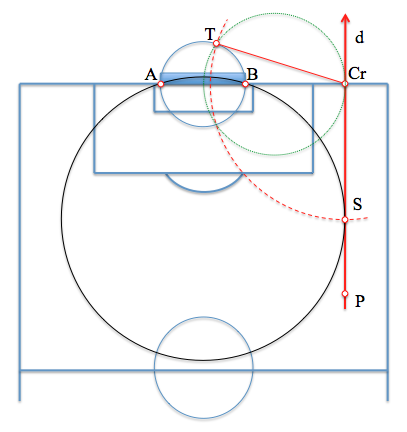
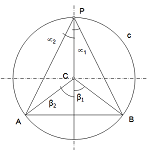
Al repasar los conceptos de "arco capaz" sobre un segmento, podemos concluir que éste punto será aquél que pertenezca a una circunferencia que pase por los puntos A y B, que a la vez sea tangente a la recta d para que su diámetro sea mínimo.

Este planteamiento nos lleva a resolver el "Problema fundamental de tangencias" en el caso de dos puntos y una recta, que solucionábamos mediante los conceptos de potencia de un punto respecto a una circunferencia.

La recta AB será el eje radical de todas las circunferencias que pasan por dichos puntos, mientras que la recta "d" lo será de todas las que son tangentes a esta recta. El punto Cr de intersección de ambas rectas tendrá igual potencia respecto de las que pasan por A y B, y las tangentes a "d", por lo que podremos determinar este valor de potencia que será la distancia al punto solución.

En la figura se ha resuelto con una circunferencia auxiliar de diámetro AB. La potencia desde Cr será igual al cuadrado del segmento de tangencia que pasará por el punto T. El punto solución, S, distará esta longitud a Cr.

Geometría Métrica

Lugares geométricos: Diferencia de cuadrados de distancias a dos puntos fijos

El estudio de los diferentes lugares geométricos que aparecen en los modelos gráficos más comunes permite comprender y estructurar las construcciones gráficas que sirven para resolver muchos problemas clásicos.

Dados dos puntos fijos, B y C en la figura, se trata de determinar las posiciones que puede ocupar el punto A para que la diferencia entre los cuadrados de la distancia desde A a dichos puntos sea constante.

Para determinar este lugar geométrico haremos uso del teorema de pitágoras. Buscaremos triángulos rectángulos y relacionaremos la longitud de sus lados (distancia entre sus vértices)  mediante este célebre teorema.

En la figura supondremos que B y C son los puntos fijos, y A pertenece al lugar geométrico buscado. La distancia "a" entre B y C es un valor constante, no varía al ser B y C dos puntos fijos. Si se determina el punto medio M de este lado y el punto H en la perpendicular desde A al lado BC, obtendremos la altura h y la mediana m del triángulo ABC.

Aplicando pitágoras a los triángulos ABH y AHC tendremos:

Que nos relaciona los cuadrados de los lados de los triángulos (distancias buscadas). Si restamos una ecuación a la otra tendremos:

Esta ecuación nos indica que si queremos que la diferencia de cuadrados sea constante, el producto 2ad debe de serlo y, como a es un valor constante, el segmento d debe permanecer invariable.

Geométricamente debe mantenerse fijo el punto H y por lo tanto el punto A, que se encuentra sobre la altura del triángulo, debe permenecer sobre una recta perpendicular a BC que pase por H.

El lugar geométrico de puntos cuya diferencia de cuadrados de distancias a dos puntos fijos es constante, es una recta perpendicular al segmento que determinan los puntos fijos.

Este lugar geométrico es de gran interés para el estudio del eje radical de dos circunferencias.

Geometría Métrica

Aplicación del teorema de Pitágoras: Ecuación de la circunferencia

Una de las primeras aplicaciones que podemos encontrar en el teorema de Pitágoras, es su uso en la determinación de la ecuación de una circunferencia.

La relación métrica entre los dos catetos de un triángulo rectángulo son esencialmente la expresión del concepto de medida euclídeo.

Los puntos de una circunferencia se encuentran a igual distancia del centro de la misma (O).

Una circunferencia es el lugar geométrico de los puntos de un plano que equidistan de otro punto fijo y coplanario llamado centro en una cantidad constante llamada radio.(W)

Para determinar la ecuación de la circunferencia analizaremos primero el caso en que ésta se encuentre con su centro en el origen del sistema de referencia, para generalizar a continuación a cualquier posición del plano.

La distancia de cualquier punto P(x,y) de la circunferencia a su centro O es igual a su radio R. En la figura se aprecia que es la hipotenusa de un triángulo rectángulo que tiene por catetos a las coordenadas x e y del punto P. Por ello, aplicando el teorema de pitágoras:

Si desplazamos el centro de la circunferencia a un punto de coordenadas (Xo, Yo), como se aprecia en la figura:

los puntos de la circunferencia seguiran a distancia R del centro, pero en este caso los catetos del triángulo ya no serán las coordenadas, sino la diferencia entre estas y las del centro. La nueva ecuación será:

Podemos desarrollar esta ecuación y agrupar los coeficientes y las variables de forma ordenada, con lo que tendremos:

O simplificar agrupando

Siendo

Una aplicación directa por lo tanto de un teorema de gran importancia en la geometría.

[caption id="" align="aligncenter" width="150"] Curso de Geometría Métrica[/caption]