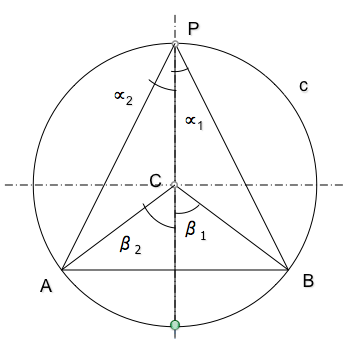
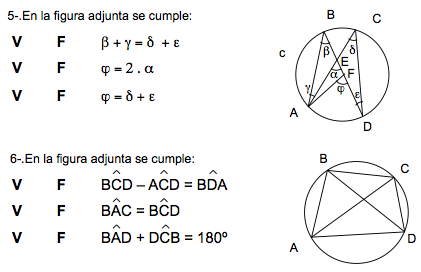
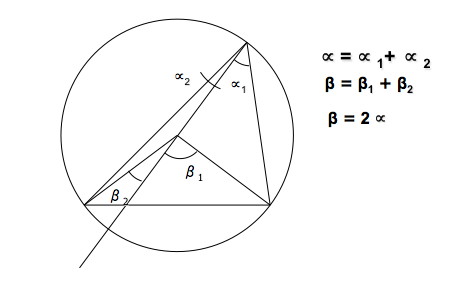Hemos visto un primer programa denominado "DrawWorld" que nos introducía la programación en JAVA orientada a los gráficos. Este módulo de programación nos ha servido para ver un primer fractal recursivo: El triángulo de Sierpisnki.
Veamos como modificar este programa elemental para generar un nuevo fractal recursivo básico: La curva de Kuch.
(Ver como se genera un fractal recursivo)
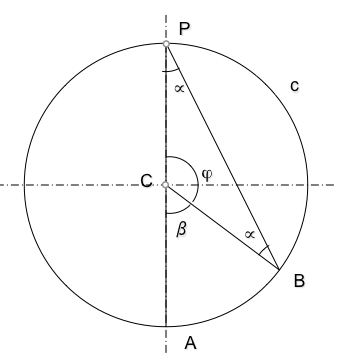
Es un fractal que se construye de forma recursiva a partir de una línea recta. Sus lados se dividen en tres partes iguales y el segmento central se cambia por dos iguales que forman 60 grados con los anteriores y entre si.
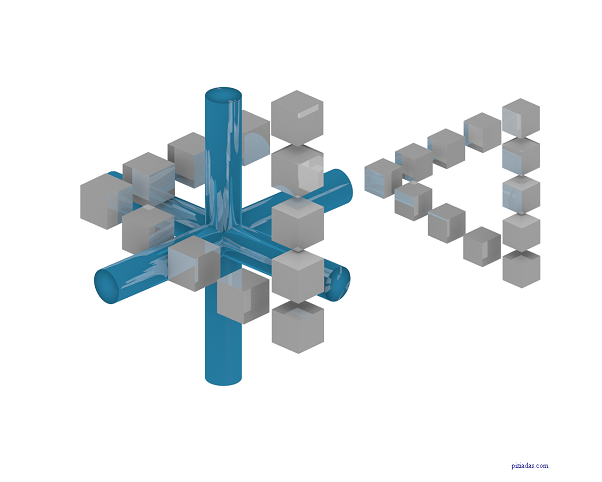
La curva de Koch, también conocida como copo de nieve es un fractal que puede obtenerse mediante diferentes procedimientos como los denominados IFS o sistemas de funciones iteradas (deterministas o no), sistemas basados en reglas, etc.
El algoritmo recursivo goza de la virtud de representar además un concepto muy asociado a los fractales: el infinito. La esencia de la recursividad permite describir de una forma muy simple la de la propia curva. Un universo que contiene a otro y este a su vez copia el patrón a menor escala (de forma contractiva) en una secuencia que se repite infinitamente.
La curva de Koch pertenece al grupo de los fractales autosimilares[1], siendo el método de obtención del tipo determinista.
[caption id="attachment_13420" align="alignleft" width="240" caption="Iniciador"]
[/caption][caption id="attachment_13421" align="alignright" width="241" caption="Primera iteración"]
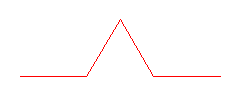[/caption]Dimensión Fractal
La dimensión de un objeto es un concepto topológico que sitúa o clasifica a los objetos en espacios métricos. La noción intuitiva de espacios con dimensiones enteras choca con las denominadas dimensiones fractales, que toman valores reales.
La curva de Peano es una curva capaz de llenar el plano. ¿Tiene por lo tanto dos dimensiones?, cabe preguntarse.
Se asocia la dimensión de un fractal con la aspereza, o fragmentación, del mismo, de manera que una dimensión mayor presentará un aspecto más rugoso o dentado. En cualquier caso da información caracterizándolo acerca de su complejidad.
La curva de Koch tiene una relación s=1/3, con n = 4, por lo que su dimensión fractal es:
D=ln4/ln3 ~ 1.269
Si cada uno de estos nuevos segmentos se dividen de nuevo de forma recursiva se obtiene la curva de Hoch
[caption id="attachment_13422" align="aligncenter" width="247" caption="curva de koch para n=2"]
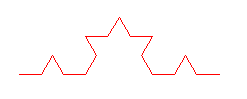[/caption].
[caption id="attachment_13423" align="aligncenter" width="215" caption="curva de koch para n=3"]
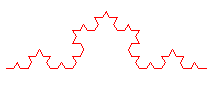[/caption][caption id="attachment_13424" align="aligncenter" width="226" caption="curva de koch para n=4"]
[/caption]Si usamos tres líneas, en lugar de una como iniciador, en forma de triángulo equilátero aparecerá la clásica forma de copo de nieve, nombre con el que se conoce a esta configuración del fractal.
[caption id="attachment_13425" align="aligncenter" width="262" caption="curva de koch : copo de nieve"]
[/caption]Algoritmo generador
Se ha definido una función "paintRecursivo" (que se llama desde el método "paint") a la que pasamos los puntos de la línea o líneas del triángulo, así como el nivel de recursividad. La función calcula los vértices de los nuevos segmentos, pinta la figura y se llama a sí misma de nuevo reduciendo el nivel de recursividad.
Por lo tanto, en cada llamada a la función se reduce el valor de recursividad, de forma que cuando éste es cero termina de efectuar la recursividad.
import java.applet.Applet;
import java.awt.Graphics;
/**
* @author José Juan Aliaga
*/
public class MainApp extends Applet {
double xp1=300;
double yp1=300;
double xp2=10;
double yp2=300;
double sin60=Math.sin(3.14/3.);
int nivel_de_recursividad=6;
public MainApp() { }
public static void main(String[] args) { }
public void paint(Graphics g){
paintRecursivo(g,nivel_de_recursividad,xp1,yp1,xp2,yp2);
}
private void paintRecursivo(Graphics g, int i, double xp12, double yp12, double xp22, double yp22 ) {
double dx=(xp22-xp12)/3.;
double dy=(yp22-yp12)/3.;
double xx=xp12+3*dx/2.-dy*sin60;
double yy=yp12+3*dy/2.+dx*sin60;
if(i<=0){
g.drawLine((int)xp12,(int)yp12,(int)xp22,(int)yp22);
}
else{
paintRecursivo(g,i-1,xp12,yp12,xp12+dx,yp12+dy);
paintRecursivo(g,i-1,xp12+dx,yp12+dy,xx,yy);
paintRecursivo(g,i-1,xx,yy,xp22-dx,yp22-dy);
paintRecursivo(g,i-1,xp22-dx,yp22-dy,xp22,yp22);
}
} }
[caption id="" align="aligncenter" width="94" caption="Curso JAVA"]
[/caption]
