Un tipo de trabajo recurrente en los blogs que han desarrollado mis alumnos ha consistido en la búsqueda e identificación de la geometría en todos los aspectos de su realidad cotidiana, dándose cuenta de la importancia de la misma.
Las curvas cónicas que se estudian en el apartado de geometría métrica tienen un alto interés en los estudios de ingeniería aeronáutica, ya que permiten describir las trayectorias de los cuerpos sometidos a las leyes gravitatorias. Sin embargo, como claramente destacan en sus trabajos, no son los únicos campos de aplicación. El breve artículo que sigue, realizado por el grupo de alumnos autodenominado "El laberinto del Ángulo" es una muestra de estas inquietudes de relación con lo cotidiano.
por AG El Laberinto del Ángulo
Seguro que ya sabes que las elipses y parábolas son curvas son muy importantes en Física ya que se ajustan perfectamente a la representación matemática de muchos fenómenos.
Pero también vemos elipses y parábolas en nuestra vida cotidiana sin que nos demos cuenta de ello. A continuación te mostramos algunos ejemplos.
- Parábola: cualquier cuerpo lanzado al aire horizontal u oblicuamente realiza una parábola bajo la acción de la gravedad.
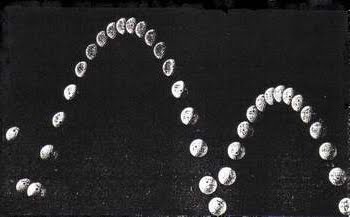
Un ejemplo es una pelota que bota desplazándose en la cual la parábola va haciendo más pequeña debido a la pérdida de energía desperdiciada en cada bote.
Otro ejemplo de bonitos arcos parabólicos son los creados por las fuentes de las ciudades sean las fuentes ‘‘Cibeles’’, ‘‘Neptuno’’o las del Paseo del Prado de Madrid.
También podemos encontrar formas parabólicas cuando un haz luminoso se proyecta cónicamente sobre una pared blanca de forma que la pared sea paralela a la generatriz del cono.
 |  |
O también en una antena parabólica (o para el seguimiento de satélites) la cual aprovecha una de las propiedades más importantes de la parábola que es cualquier rayo que incida de forma paralela al eje de la parábola rebota en su superficie pasando por el foco concentrando los rayos en este punto. También es el caso del faro del coche, cocina solar...
 |  |
- Elipse: es la curva que describen los planetas en su giro alrededor del sol pero también podemos encontrarlas a nuestro alrededor aunque es difícil pero solo aparentemente.
Algunos ejemplos son las plazas con ''forma elíptica'' que podemos encontrar en ciudades como Madrid o Bilbao pero sin duda la más famosa e impresionante es la Plaza de San Pedro en el Vaticano.
O también la iglesia del Monasterio de San Bernardo en Alcalá de henares (Madrid) ,más conocido como ''Las Bernardas''. Un templo de una única nave y planta elíptica con cúpula del mismo trazado.
Bibliografía: www.elrincóndelaciencia.com
