Fundamentos proyectivos
Un sistema lógico axiomático parte de la definición de un reducido número de elementos básicos que se relacionan mediante un conjunto de reglas. La aplicación de estas reglas permite inferir propiedades o teoremas que a su vez son útiles para generar nuevas propiedades.
Se genera de esta forma un conjunto amplio de relaciones a partir de unas definiciones básicas (elementos) y un limitado número de reglas (axiomas).
Las reglas de inferencia son las operaciones proyectivas que relacionan a los elementos.
Los elementos básicos de la geometría clásica son los puntos, las rectas y los planos. Es posible definir nuevas geometrías con otros elementos básicos y diferentes operaciones y axiomas.
Estos elementos son los números de la geometría, y pueden ser usados, junto con las transformaciones gráficas como operadores, para idealizar y describir los modelos de la realidad.
Los elementos pueden pertenecer a un espacio unidimensional, bidimensional, tridimensional ...
Las figuras geométricas se forman a partir de los elementos básicos, por lo que interesa el estudio de sus posibles relaciones. En particular el enfoque basado en los invariantes conduce a un modelo de pensamiento que agrupa los conceptos en función de su independencia en la aplicación a la resolución de los problemas.
La razón simple y la razón doble, como se verá más adelante, permiten establecer nuevos modelos de solución en problemas que se han tratado normalmente desde una perspectiva pitagórica, en la que las medidas absolutas de las distancias, y no tanto sus relaciones con otras, constituyen el elemento argumental.
Al operar con estos elementos, los restantes deben considerarse agrupaciones de los primeros. Por ejemplo, si el elemento base es el punto, la recta y el plano deben reducirse a conjuntos de puntos; la recta debe entenderse como un conjunto de infinitos puntos que se pueden determinar con un simple parámetro o coordenada respecto de un punto origen,; el plano como un conjunto de infinitos puntos determinados mediante dos parámetros de un sistema de coordenadas.
[caption id="" align="aligncenter" width="320" caption="El lenguaje geométrico"]
[/caption]
Esta forma de relacionar los elementos permite generalizar los teoremas obtenidos para un elemento dado, al resto de elementos.
La ley de dualidad recoge esta idea aportando un mecanismo semántico para este fin. Un simple cambio de palabras en un teorema sobre rectas, puede convertirse en otro para planos o para puntos simplificando mediante abstracción lógica la estructura geométrica.
Elementos y Formas geométricas
Los elementos geométricos se pueden estructurar en grupos que los contienen y que se denominan formas geométricas.
Por ejemplo, los elementos (puntos) del espacio tridimensional R3 que distan una longitud constante de otro dado determinan la forma geométrica denominada esfera. Los que equidistan de una recta determinarían un cilindro o superficie cilíndrica de revolución, y los que se encuentran a igual distancia de un plano formaran dos nuevos planos paralelos al anterior, etc.
Se puede utilizar una semántica que generaliza los conceptos independientemente de la naturaleza de los elementos básicos constitutivos. Obsérvese la “forma dual” en que se presentan los siguientes enunciados.
Una línea puede ser entendida como un elemento geométrico básico o como un conjunto de infinitos puntos.En este segundo caso diremos que la recta es la base de la forma geométrica denominada “Serie rectilínea”. |
Un punto puede ser entendido como un elemento geométrico básico o como la intersección de infinitas rectas.En este segundo caso diremos que el punto es el vértice (base) de la forma geométrica denominada “Haz de rectas”. |
La “Serie rectilínea”, “Haz de rectas” y el “Haz de planos” son las formas geométricas más básicas. Sus elementos son puntos, rectas y planos respectivamente.
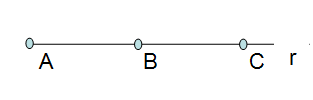
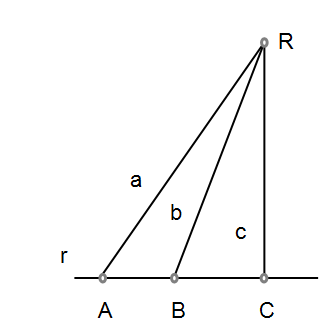
Serie rectilínea La forman los infinitos puntos de una recta. |
 |
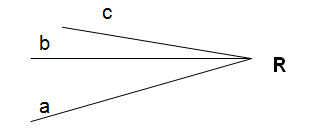
Haz de rectas Lo forman las infinitos rectas de igual vértice. |
 |
Haz de planos Los forman los infinitos planos que comparten una recta |
 |
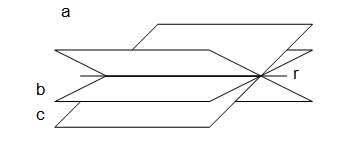Tabla 1 Formas de primera categoría
[caption id="attachment_13573" align="aligncenter" width="400" caption="Sistemas_de_representacion"]
[/caption]
La geometría se presenta en los elementos que constituyen la naturaleza. Las formas cotidianas se pueden describir con modelos gráficos geométricos simples. Convivimos por tanto con la geometría de forma cotidiana sin prestarle demasiada atención.
¿En qué se parecen un tornillo, una galaxia y un caracol?
Literalmente significa vejiga (vesica), que al llenarse de aire adquiere la forma de pez (piscis). Era el diagrama central de la Geometría Sagrada en el misticismo cristiano de la Edad Media. Representa simbólicamente a Cristo.
