[/caption]La homotecia es una transformacion homográfica que conserva las relaciones de medida entre cada par de segmentos homotéticos u homólogos.
Conserva el paralelismo entre una línea y su transformada, por lo que determina figuras semejantes y mantiene las relaciones angulares (es conforme).
Su principal aplicación en geometría es la determinación de problemas con relaciones de áreas en figuras semejantes; también es de utilidad para la resolución de algunos ejercicios de tangencias.
Dos figuras semejantes tienen la misma forma y diferente área
[caption id="attachment_13991" align="aligncenter" width="240" caption="Homotecia"]
[/caption]Se basa en los conceptos de semejanza que vimos en el teorema de Thales; no es una transformación involutiva y no puede tener elementos dobles salvo el centro. Pertenece al grupo de las transformaciones afines.
Definición de la transformación
La homotecia es una transformación con centro. Esto significa que un punto y su transformado se encuentran alineados con el centro de homotecia o semejanza, de forma análoga a la transformación conocida como inversión que se verá posteriormente.
La relación entre las posiciones relativas de cada punto y su transformado respecto del centro de homotecia se basan en el concepto de semejanza.
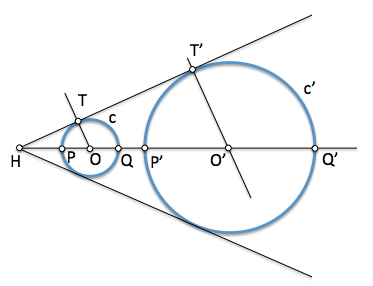
Dado un centro "H", y un par de puntos homólogos "P" y "P'", el cociente de las distancias de estos puntos al centro de homotecia es constante y se denomina razón de homotecia.
HP / HP' = HQ / HQ' = HT / HT' = K
[caption id="attachment_13989" align="aligncenter" width="373" caption="Circunferencias homotéticas"]
[/caption]Centros de homotecia entre dos circunferencias
Relacionar mediante esta transformación dos circunferencias es de especial interés para su aplicación en los problemas de tangencias, así como para el posterior estudio de otra transformación: la inversión.
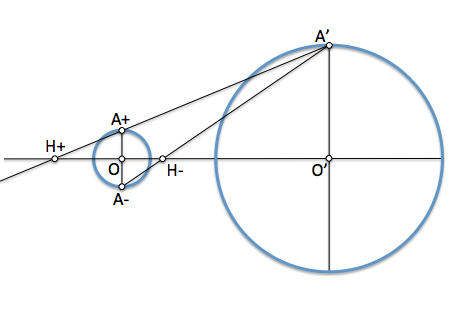
Si suponemos que dos circunferencias son homotéticas, los puntos situados sobre radios paralelos deben ser homólogos. Dependiendo del sentido del radio tendremos transformaciones de razón positiva (los dos radios en el mismo sentido) o negativa (diferente sentido). Los centros positivo, H+, y negativo, H-, deben encontrarse sobre las rectas que unen cada par de puntos homólogos (A-A') así como en la línea que une los centros de las circunferencias ya que también son homotéticos.
[caption id="attachment_13992" align="aligncenter" width="460" caption="Centros de homotecia de dos circunferencias 1"]
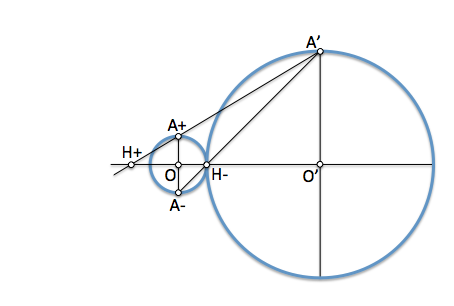
[/caption]Podemos ver como en algunas posiciones particulares alguno de los centros de homotecia puede estar situado sobre las propias circunferencias, como es el caso en el que éstas son tangentes entre sí.
[caption id="attachment_13993" align="aligncenter" width="454" caption="Centros de homotecia de dos circunferencias 2"]
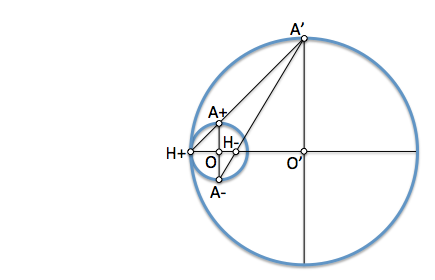
[/caption]Si una es interior a la otra veremos además que el otro centro de homotecia es interior a ambas circunferencis.
[caption id="attachment_13994" align="aligncenter" width="435" caption="Centros de homotecia de dos circunferencias 3"]
[/caption]Aplicación de la homotecia a los problemas de tangencias
Una de las posibles aplicaciones de esta transformación es la determinación de circunferencias con condiciones de tangencia respecto de dos rectas.
Supongamos el siguiente ejercicio:
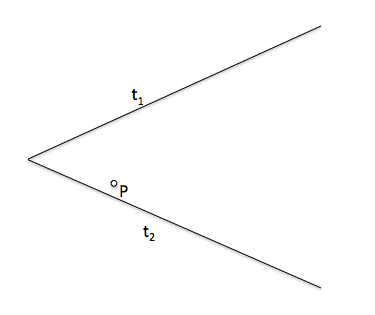
Determinar las circunferencias tangentes a dos rectas y que pasan por un punto P
[caption id="attachment_13997" align="aligncenter" width="375" caption="Homotecia - Problema de tangencias"]
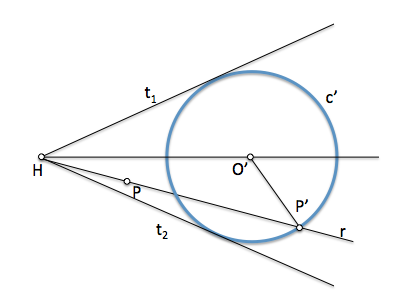
[/caption]Si suponemos que el punto de intersección de las rectas tangentes es un centro de homotecia, H, podemos convertir la circunferencia que buscamos con una razón cualquiera en otra circunferencia que debe ser tangente a dichas rectas. Para realizar esta transformación elegiremos un radio cualquiera para esta nueva circunferencia
[caption id="attachment_13998" align="aligncenter" width="402" caption="Homotecia - Problema de tangencias planteado"]
[/caption]El punto P debe tener un punto homólogo, P', en la nueva circunferencia. Este punto se encontrará en la intersección de esta circunferencia auxiliar y la recta r que pasa por P y por el centro H de homotecia (Nótese que puede haber otro punto de intersección de r con c', válido para obtener una segunda solución).
[caption id="attachment_13999" align="aligncenter" width="409" caption="Homotecia - Problema de tangencias solucionado"]
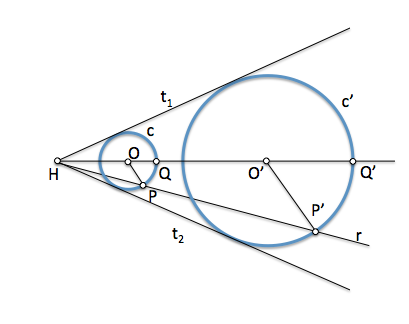[/caption]El centro de la circunferencia solución lo determinamos obteniendo el radio homólogo del que pasa por P', que pasará por el punto P y será paralelo al anterior.
No hay comentarios:
Publicar un comentario