Clásicamente los problemas de tangencias se han estudiado buscando construcciones geométricas propias de cada caso de estudio.
Los conceptos de potencia de un punto respecto de una circunferencia permiten abordar los problemas con un enfoque unificador, de forma que cualquier enunciado de tangencias o incidencias en general se puede reducir a uno más genérico que denominaremos problema fundamental de tangencias (PFT).
El PFT puede enunciarse como el problema de determinación de una circunferencia que pasa por dos puntos y es tangente a una recta o bien a otra circunferencia.
Un mayor grado de abstracción permitiría sustituir los puntos de paso por una condición de pertenencia a un haz, aunque este enfoque lo dejaremos pendiente para más adelante.
Resolveremos el primer caso de estudio enunciando el problema como:
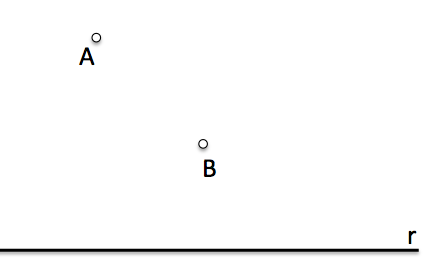
Determinar las circunferencias que pasan por los puntos A y B y son tangentes a la recta r
[caption id="attachment_13882" align="aligncenter" width="431" caption="Datos para definir el Problema fundamental de tangencias"]
[/caption]Análisis del problema fundamental de tangencias
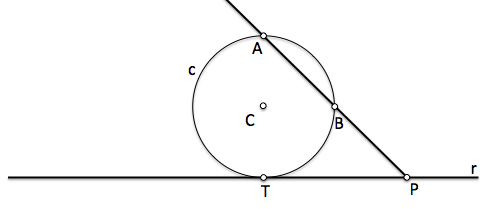
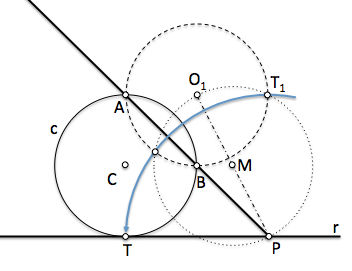
En la figura de análisis se aprecia que la circunferencia c de centro C puede ser una de las soluciones del problema ya que pasa por los puntos A y B y es tangente a la recta r. En esta figura ,en la que representamos la circunferencia solución que estamos buscando, podemos determinar propiedades que servirán para deducir una construcción que nos permita determinarla.
[caption id="attachment_13884" align="aligncenter" width="490" caption="Fundamentos del problema fundamental de tangencias PFT"]
[/caption]La recta que pasa por los puntos A y B corta a la recta r en un punto P. La potencia de este punto respecto de la circunferencia es:
[caption id="attachment_13885" align="aligncenter" width="117" caption="Potencia de un punto"]
[/caption]De la expresión anterior deducimos que si obtenemos el valor del segmento PT (raiz de la potencia) podemos obtener el punto T de tangencia y el problema se reduce a determinar la circunferencia que pasa por tres puntos: A, B y T (su centro estará en la intersección de dos mediatrices).
Resolución del problema.
Determinaremos el valor de la potencia por medio de una de las construciones usadas para resolver medias proporcionales:
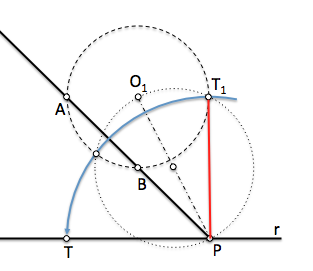
Como la potencia del punto P respecto de cualquier circunferencia que pase por los puntos A y B es la misma, podemos utilizar una circunferencia auxiliar de cualquier radio que pase por estos puntos, como la representada en la figura de centro O1, situado en la mediatriz de A y B.
El valor de la potencia lo determinaremos obteniendo el segmento de tangencia desde P a esta circunferencia auxiliar; para ello, construiremos un arco capaz de 90 grados sobre el segmento PO1
[caption id="attachment_13887" align="aligncenter" width="313" caption="Resolucion problema fundamental de tangencias"]
[/caption]El valor del segmento de tangencia ( P-T1) lo llevaremos sobre la recta r para determinar el punto T de tangencia mediante un simple giro de centro en P.
[caption id="attachment_13891" align="aligncenter" width="352" caption="Solución del PFT"]
[/caption]Número de soluciones
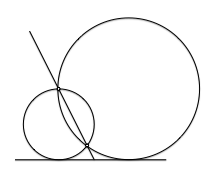
Dependiendo de la dirección en que llevemos el segmento PT obtendremos una u otra de las dos posibles soluciones al problema.
[caption id="attachment_13889" align="aligncenter" width="209" caption="Dos soluciones"]
[/caption]
No hay comentarios:
Publicar un comentario